Spatial filtering

Various reasons why you might want to apply spatial filters: low pass filters to get rid of cosmic rays/bad pixels, high pass filters to look for features. Many techniques possible. Generally, in other fields, people often filter in Fourier domain, but doesn't seem to be so useful in astronomy.

Low pass filtering: smoothing, median filtering.

High pass filtering: unsharp masking.

Edge detection.

Object recognition.

Deconvolution

To remove known PSF. Problem: noise.

If you know expected profile of model, you're better off convolving and fitting, e.g. psf fitting. Sometimes, however, you don't. If you're going to fit a model to a deconvolved image, strongly consider fitting a convolved model to the data instead.

Fourier deconvolution: since observed function is convolution of true signal with response function, we have:

$$S(f) = R(f) U(f)$$

where $U$ is true signal, $R$ is response function, $S$ is observed signal. Consequently, just FFT observed and response functions, divide, and IFFT.

However, in reality there is noise, so we can't directly get $U$.

$$O(f) = S(f) + N(f)$$

where $O$ is the observed signal. Instead we want to get our best estimate of $U$:

$$U\prime(f) = {O(f)\Phi(f)\over R(f)}$$

where $\Phi$ is some filter we apply to eliminate the noise. What should we choose for $\Phi$? From least squares considerations, one can derive the Wiener filter:

$$\Phi(f) = {\vert S(f)\vert^2\over \vert S(f)\vert^2 + \vert N(f\vert^2}$$

where the interpretation is easy to see graphically. However, to do this, we need to estimate $S(f)$. Either know noise properities a priori, or take power spectrum and estimate them.

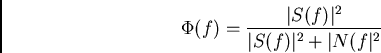
Lucy deconvolution: guess image, convolve with PSF, take ratio of image to model, convolve ratio with PSF transpose, use this to update model. Iterate.

Maximum entropy.

Beware that some deconvolution schemes do not preserve flux.