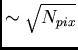Surface photometry

What if we have extended (resolved) objects? Can talk about either integrated or surface brightnesses. If integrated brightnesses, use some sort of aperture, remember aperture corrections (though you probably can't estimate them very well, and they probably don't matter too much).

For surface brightnesses, just look at fluxes per area on sky. Remember that there will be some mixing from PSF/seeing; topic of extracting most spatial information will be discussed next time. Counts/pixel go directly to mag/square arcsec using stellar calibration, size of pixels.

If object is irregular, not much more you can do. Hard to observe faint irregular objects accurately because of S/N. However, if object has some degree of regularity (e.g., galaxies), one can average over regions to increase S/N substantially. Generally, many galaxies can be fairly well parameterized by elliptical isophotes, so if you can determine ellipse parameters, you can average along a given isophote to increase S/N by $\sim \sqrt{N_{pix}}$.

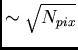Note that if all isophotes are concentric and have same ellipticity, one could use elliptical aperture photometry. But many galaxies have twisting isophotes, so often one needs to solve for varying ellipticity and position angle as a function of semimajor axis.

Several methods for doing this have been presented by Kent (ApJ 266, 562) and Lauer (ApJ 311, 34). They are similar in that they solve for elliptical isophotes using nonlinear least squares. Both start with some a priori guess of isophote parameters. Kent method solves for Fourier coefficients which parametrize (observed-guess) ellipse; ellipse parameters modified to minimize $A_1, B_1, A_2, B_2$:

$$I = I_0 + A_1 cos E + B_1 sin E + A_2 cos 2E + B_2 sin 2E + \cdots$$

where $E$ is the eccentric anomaly:

$$x = a_0 cos E$$

$$y = a_0 sin E (1-\epsilon_0)$$

If image is perfectly elliptical, then all higher order terms vanish. For this method, one needs to choose a set of ellipses (semimajor axes) and sample them in the data. Generally, these are spaced by $\sim$ one pixel in semimajor axis: this is good for spatial resolution but can be poor for S/N.

Lauer describes galaxy as having power law surface brightness profile with constant ellipticity/position angle between some a priori specified semimajor axes.

$$G(x,y) = \mu_k ({r\over d_k})^\gamma$$

$$\gamma = log ({\mu_{k+1}\over \mu_k}) / log ({d_{k+1}\over d_k})$$

$$d_k = a_k (1-\epsilon_k) [sin^2 (\phi_k - \theta_k) + (1-\epsilon_k)^2 cos^2 (\phi_k - \theta_k)]^{-1/2}$$

All pixels are included in fit and parameters are adjusted by nonlinear least squares.

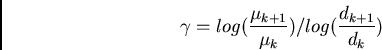
How to obtain. Calibration.

Surface photometry, integrated photometry and variable pixel area effects.