Dispersing elements

Prisms

Perhaps the simplest conceptual dispersing element is a prism, which disperses light because the index of refraction of many glasses is a function of wavelength. From Snell's law, one finds that:

$${d\theta\over d\lambda} = {t\over d} {dn\over d\lambda}$$

where $t$ is the base length, and $d$ is the beamwidth. Note that prisms do not have anamorphic magnification ($r = 1$). The limiting resolution of a prism, from above is:

$$R_{max} = {d_2 \over f_2 (d\lambda/dx)} = d_2 {d\theta\over d\lambda}$$

$$R_{max} = t {dn\over d\lambda}$$

One finds that $dn/d\lambda \propto \lambda^{-3}$ for many glasses.

So dispersion and resolution are a function of wavelength for a prism. In addition, the resolution offered by a prism is relatively low compared with other dispersive elements (e.g. gratings) of the same size. Typically, prisms have $R<1000$. Consequently, prisms are rarely used as the primary dispersive element in astronomical spectrographs. They are occasionally used as cross-dispersing elements.

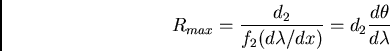
Gratings

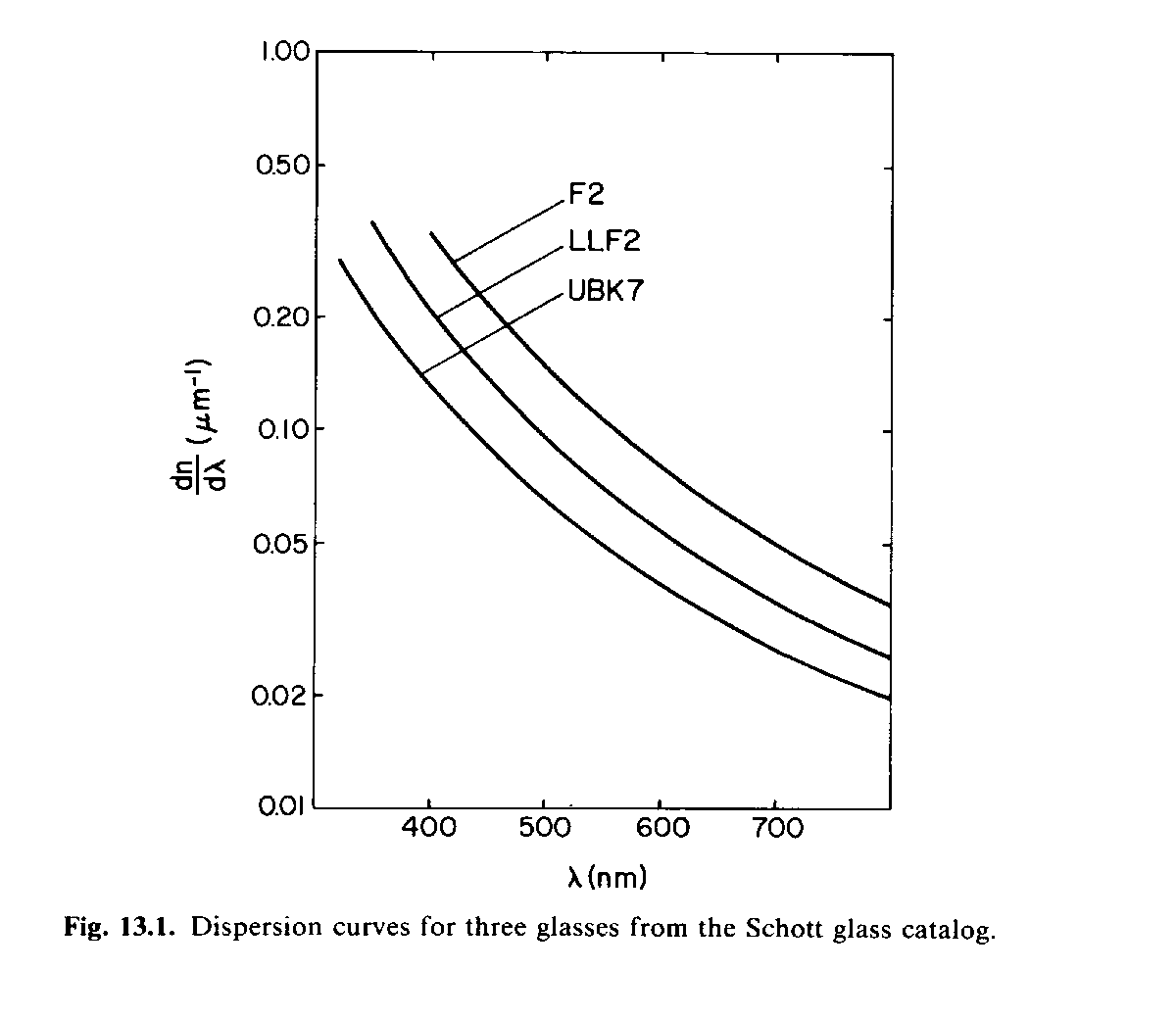
Diffraction gratings work using the principle of multi-slit interference. A diffraction grating is just an optical element with multiple grooves, or slits. Diffraction gratings may be either transmissive or reflective. Bright regions are formed where light of a given wavelength from the different slits constructive interferes.

The location of bright images is given by the grating equation:

$$m\lambda = \sigma (sin \theta + sin \alpha)$$

for a reflection grating, where $\sigma$ is the groove spacing, $m$ is the order, and $\alpha$ and $\theta$ are the angles of incidence and diffraction as measured from the normal to the grating surface.

The dispersion of a grating can then be derived:

$${d\theta\over d\lambda} = {m\over \sigma \cos\theta}$$

One can see that the dispersion is larger at higher order, and for a finer ruled grating. The equation can be rewritten as

$${d\theta\over d\lambda} = {\sin\theta + \sin \alpha \over \lambda \cos\theta}$$

from which it can be seen that high dispersion can also be achieved by operating at large values of $\alpha$ and $\theta$. This is the principle of an echelle grating, which has large $\sigma$, and operates at high $m$, $\alpha$ and $\theta$, and gives high dispersion and resolution.

Typical gratings have groove densities between 300 and 1200 lines/mm. Echelle gratings have groove densities between 30 and 300 lines/mm.

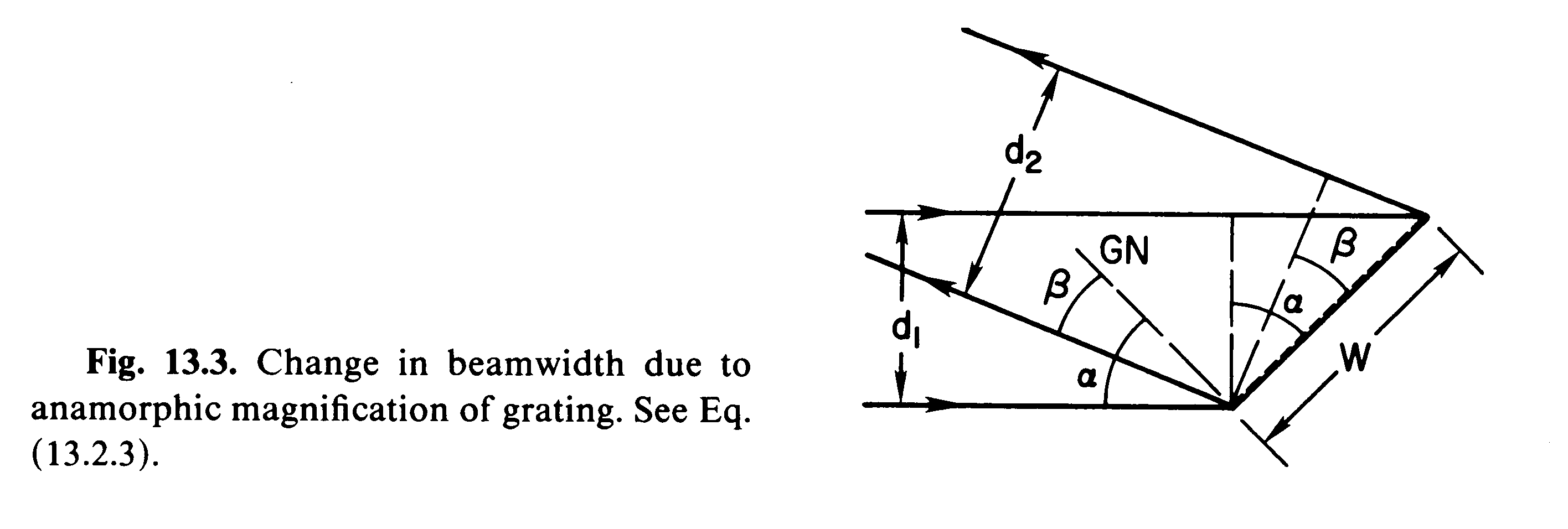
One can derive the anamorphic magnification for a grating by looking at how $\theta$ changes as $\alpha$ changes at fixed $\lambda$. One finds that:

$$r = {d\theta\over d\alpha} = {\cos \alpha\over \cos \theta} = {d_1\over d_2}$$

where the $d$'s are the beam diameters. Note that higher resolution occurs when $r<1$, or $\theta<\alpha$.

The limiting resolution can be derived:

$$R_{max} = {d_2 \over f_2 (d\lambda/dx)} = d_2 {d\theta\over d\lambda}$$

$$R_{max} = {d_2 m\over \sigma \cos\theta} = {m W\over \sigma} = m N$$

where $W$ is the width of the grating ( $=d_2/\cos\theta$), and $N$ is the total number of lines in the grating.

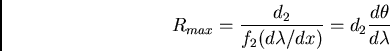
Note that light from different orders can fall at the same location, leading to great confusion! This occurs when

$$m\lambda^\prime = (m+1)\lambda$$

or

$$\lambda^\prime - \lambda = {\lambda\over m}$$

The order overlap can be avoided using either an order-blocking filter or by using a cross-disperser. The former is more common for small $m$, the latter for large $m$.

One can compare grating operating in low order, those operating in high order, and prisms, and one finds that higher resolution is available from grating, and that echelles offer higher resolution than typical low order gratings.

We can also discuss grating efficiency, the fraction of incident light which is directed into a given diffracted order. One finds that for a simple grating, less light is diffracted into higher orders. However, one can construct a grating which can maximize the light put into any desired order by blazing the grating, which involves tilting each facet of the grating by some blaze angle. The blaze angle is chosen to maximize the efficiency at some particular wavelength in some particular order; it is set so that the angle of diffraction for this order and wavelength is equal to the angle of reflection from the grating surface.