Spectrographs

A spectrograph is an instrument which separates different wavelengths of light so they can be measured independently. Most spectrographs work by using a dispersive element, which directs light of different wavelengths in different directions.

A conventional spectrograph has a collimator, a dispersive element, a camera to refocus the light, and a detector. The performance of a spectrograph is characterized by the dispersion, which gives the amount that different wavelengths are separated, and the resolution, which gives the smallest difference in wavelength that two different monochromatic sources can be separated. There are different sorts of dispersive elements with different characteristics; two common ones are prisms and diffraction gratings, with the latter the most commonly in use in astronomy.

The dispersion depends on the characteristic of the dispersing element. Various elements can be characterized by the angular dispersion, $d\theta/d\lambda$, or alternatively, the reciprocal angular dispersion, $d\lambda/d\theta$. In practice, we are often interested in the linear disperion, $dx/d\lambda = f_2 d\theta/d\lambda$ or the reciprocal linear dispersion, $d\lambda/dx = {1\over f_2} d\lambda/d\theta$ where the latter is often referred to simply as the dispersion in astronomical contexts, and is usually specified in Å/mm or Å/pixel.

If the source being viewed is extended, it is clear that any light which comes from regions parallel to the dispersion direction will overlap in wavelength with other light, leading to a very confused image to interpret. For this reason, spectrographs are usually used with slits or apertures in the focal plane to restrict the incoming light. Note that one dimension of spatial information can be retained, leading to so-called long-slit spectroscopy. Also, if there is a single dominant point source in the image plane, or if they are spaced far enough (usually in combination with a low dispersion) that spectra will not overlap, spectroscopy can be done in slitless mode. However, note that in slitless mode, one can be significantly impacted by sky emission.

The resolution depends on the width of the slit or on the size of the image in slitless mode, because all a spectrograph does is create an image of the focal plane after dispersing the light. The ``width'' of a spectral line will be given by the width of the slit or the image, whichever is smaller. In reality, the spectral line width is a convolution of the slit/image profile with diffraction and the disperser response function. Note that throughput may also depend on the slit width, depending on the seeing.

Given a linear slit or image width, $\omega$ (or an angular width, $\phi = \omega/f$, where $f$ is the focal length of the telescope) and height $h$ (or $\phi^\prime = h/f$), we get an image of the slit which has width, $\omega^\prime$, and height, $h^\prime$, given by

$$h^\prime = h {f_2\over f_1}$$

$$\omega^\prime = r \omega {f_2\over f_1}$$

where we have allowed that the dispersing element might magnify/demagnify the image in the direction of dispersion by a factor $r$, which is called the anamorphic magnification.

Using this, we can derive the difference in wavelength between two monochromatic sources which are separable by the system.

$$\delta\lambda = \omega^\prime {d\lambda\over dx}$$

$$\delta\lambda = r \omega {f_2\over f_1} {d\lambda\over dx}$$

The bigger the slit, the lower the resolving power.

The resolution is usually characterized in dimensionless form by

$$R\equiv {\lambda\over \delta\lambda} = {\lambda f_1 \over r \omega f_2 (d\lambda/dx)}$$

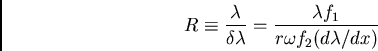
Note that there is a maximum resolution allowed by diffraction. This resolution is given aproximately by noting that minimum angles which can be separated is given by approximately $\lambda/d_2$, where $d_2$ is the width of the beam at the camera lens, from which the minimum distance which can be separated is:

$$\omega_{min} = f_2 {\lambda\over d_2}$$

The slit width which corresponds to this limit is given by:

$$\omega^\prime = r \omega {f_2\over f_1} = f_2 {\lambda\over d_2}$$

or

$$\omega = {f_1 \over r} {\lambda\over d_2}$$

and the maximum resolution is

$$R_{max} = {d_2 \over f_2 (d\lambda/dx)} = d_2 {d\theta\over d\lambda}$$

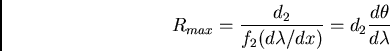
Image slicers: preserving resolution and flux.

Fiber spectrographs: multiobject data.

Slitlets: multiobject data.