- The rectangle function,
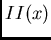 is defined such that
is defined such that
Question: what would 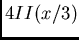 look like? How about
look like? How about 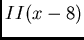 ?
?
This function when multiplied with another function provides an easy
way to cut out sections of other functions.
Question: what would
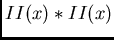 look like?
look like?
- The sinc function
This is the filtering or interpolating function; this looks almost,
but not quite like a sinusoid of gradually decreasing amplitude. (Plot
it!). Its properties include:
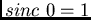
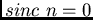 where
where 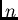 is a non-zero integer
is a non-zero integer
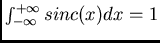
The 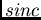 function is very important. It is the FT of the
function is very important. It is the FT of the  function, thus sinc(x) has all frequencies present with equal
strength, up to a cutoff frequency. This function, in a convolution,
therefore performs perfect low-pass filtering (as we will see when
discussing the various theorems). It is also an important
interpolation function. If the rectangle function is seen as a single
narrow slit (where the width of the slit corresponds to the
width of the rectangle function),
function, thus sinc(x) has all frequencies present with equal
strength, up to a cutoff frequency. This function, in a convolution,
therefore performs perfect low-pass filtering (as we will see when
discussing the various theorems). It is also an important
interpolation function. If the rectangle function is seen as a single
narrow slit (where the width of the slit corresponds to the
width of the rectangle function), 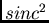 describes the Fraunhofer
diffraction pattern of a monochromatic light beam falling through the
slit. This illustrates in a simple way the Fourier relation between
``apertures'' and the resulting ``images'' produced by telescopes.
describes the Fraunhofer
diffraction pattern of a monochromatic light beam falling through the
slit. This illustrates in a simple way the Fourier relation between
``apertures'' and the resulting ``images'' produced by telescopes.
The two-d analog of the sinc (hence the FT of a square rectangle
function in x,y plane) is a Bessel function of the first order. In
optics you will learn more about the corresponding analogs of a round
2-d rectangle function (which can be seen as a round telescope
mirror).
- Impulse symbol or
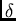 -function. Defined by
-function. Defined by
Note: this function is only defined in an integral, and you should
not interpret this as
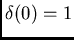 !
!
The role of 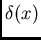 is quite important; any signal narrower than
the resolving power of your instrument or telescope is essentially
seen as an impulse function, in a mathematical sense. The function
also plays an important role in sampling. The FT of
is quite important; any signal narrower than
the resolving power of your instrument or telescope is essentially
seen as an impulse function, in a mathematical sense. The function
also plays an important role in sampling. The FT of 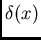 is a
function that is 1 everywhere (an infinitely sharp function has all
frequencies present at equal strength).
is a
function that is 1 everywhere (an infinitely sharp function has all
frequencies present at equal strength).
Question: what is
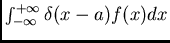 ?
?
Question: what is
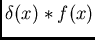 ?
?
- Sampling or replicating symbol,
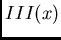 . This is an
infinite sequence of unit impulses, or delta functions:
. This is an
infinite sequence of unit impulses, or delta functions:
and
.
Thus, multiplication with 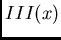 is equivalent to sampling of the
function f(x) at regular intervals. How do we control the interval
spacing?
is equivalent to sampling of the
function f(x) at regular intervals. How do we control the interval
spacing?
This function is relevant, since in practise we always sample a signal
and are never able to measure it completely. Likewise, any
reproduction of a singal or data in the computer involves a digitized,
sampled representation of the actual data, so all data is
sampled. Under convolution, 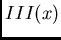 has a replicating property,
reproducing multiple, possibly overlapping, copies of f(x). Try to
sketch this yourself. Overlapping will occur if
has a replicating property,
reproducing multiple, possibly overlapping, copies of f(x). Try to
sketch this yourself. Overlapping will occur if 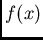 extends beyond
extends beyond
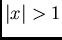 . What happens if we convolve
. What happens if we convolve 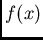 with
with 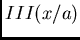 , for
different values of
, for
different values of 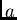 ?
?
The FT of 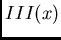 is
is 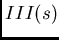 !
!
- We will not prove any of the theorems. If you are curious,
Bracewell does this in his book.
- The FT of a Gaussian function is another Gaussian. A narrow
Gaussian in one domain will have broad FT, and vice versa. Likewise,
any ``narrow'' function will have a ``broad'' FT. Taking this in the
limit, one can approximate a the
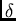 function as an ever
narrowing Gaussian of unit integral, and realize that the FT will
approach an infinitely broad Gaussian, i.e. a function that is one
everywhere, as we stated earlier.
function as an ever
narrowing Gaussian of unit integral, and realize that the FT will
approach an infinitely broad Gaussian, i.e. a function that is one
everywhere, as we stated earlier.
- We can generalize the issue of the relation between the width
of one function and that of its FT in the Similarity Theorem:
If 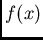 has FT
has FT 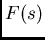 then
then 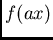 has FT
has FT
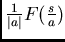 .
.
- Addition Theorem:
If 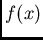 and
and 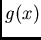 have FTs
have FTs 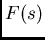 and
and 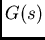 , respectively, then
, respectively, then
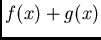 has FT
has FT 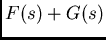 .
.
- Shift Theorem:
If 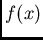 has FT
has FT 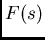 , then
, then 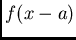 has FT
has FT
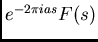 .
.
This implies that a linear shift in one domain corresponds to a phase
shift in the FT domain. This makes sense; you are not really changing
the frequency content of a function by shifting it, so the amplitude
of the FT should not change, only its phase. This theorem finds many
examples in optics and radio interferometry; consider a parallel light
beam falling on an aperture. To shift the diffracted beam through a
small angle, one changes the angle of incidence (i.e. one changes the
phase of the illumination across the aperture).
- Convolution Theorem:
If 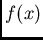 has FT
has FT 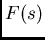 and
and 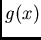 has FT
has FT 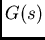 , then
, then
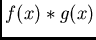 has FT
has FT 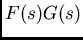 .
.
So, convolution in one domain corresponds to multiplication in the
Fourier domain. This theorem makes it often quite easy to visualize
the effects of convolutions or FTs, and also to obtain an impression
of the FT of complex functions. Often a function can be seen as one or
more products or convolutions of simple functions, and successive
application of this theorem then makes it easy to visualize what
happens in the Fourier domain. Example: an interferometer consisting
of multiple dishes can be seen as a single telescope in which many
``holes'' have been cut, or as a replication of many single
telescopes. The impact on the subsequent telescope beam (or PSF),
which is related to the FT of the aperture plane, can be seen by
applying this theorem.
- Properties related to the convolution theorem:
- Rayleighs Theorem: The integral of the squared modulus of
a function is equal to the integral of the squared modulus of its
spectrum:
.
Essentially, this is a statement of energy conservation.
- Autocorrelation Theorem: If
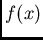 has FT
has FT 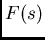 , then
its autocorrelation function
, then
its autocorrelation function
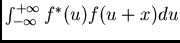 has FT,
has FT, 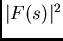 . This is a special case of the
convolution theorem. So, the autocorrelation of a signal is the FT of
its power spectrum. Some instruments work by recording the
autocorrelation of a signal rather than the signal itself (in radio
astronomy). By taking the FT of that, one has the power spectrum of
the signal. Note that phase information is lost in the
auto-correlation or power spectrum, so this is not as informative as
recording the actual signal.
. This is a special case of the
convolution theorem. So, the autocorrelation of a signal is the FT of
its power spectrum. Some instruments work by recording the
autocorrelation of a signal rather than the signal itself (in radio
astronomy). By taking the FT of that, one has the power spectrum of
the signal. Note that phase information is lost in the
auto-correlation or power spectrum, so this is not as informative as
recording the actual signal.
- Finally, an important property: The definite integral of a
function from
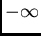 to
to 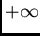 is equal to the value of its
FT transform at the origin:
is equal to the value of its
FT transform at the origin:
.
A consequence of this is that in the case of an interferometer that
does not include the ``zero spacing'', hence the 0-meter baseline, the
net total recorded flux will be zero. In radio interferometry one
speaks of the ``missing short baseline problem.''
![]() over the entire range of
over the entire range of ![]() is
finite, and any discontinuities in
is
finite, and any discontinuities in ![]() are finite.
are finite.
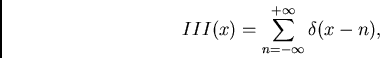
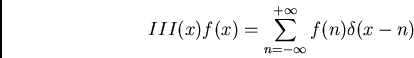
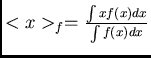 .
.