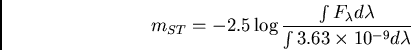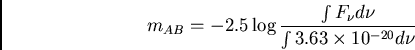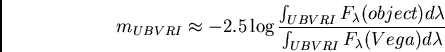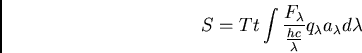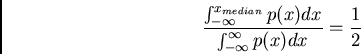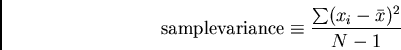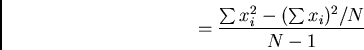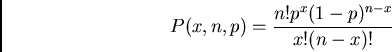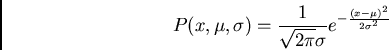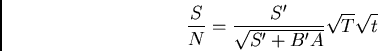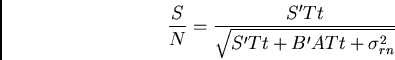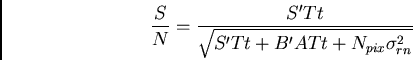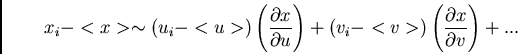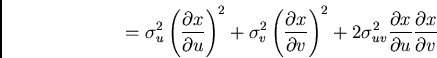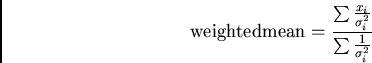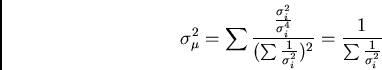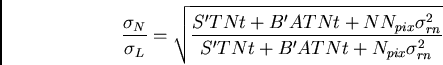

Next: Intermezzo on Fourier Transforms,
Up: AY535 class notes
Previous: Class introduction
Properties of light
- astronomy - learn about objects outside of our atmosphere.
need information from them to do so: light!
- We can describe the amount of light an object emits or that we
receive by three fundamental quantities: luminosity, L, intensity or
surface brightness, I, and flux F. Each of these can be defined
monochromatically, e.g.
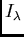 , or
, or 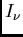 , or in integrated form
where e.g.
, or in integrated form
where e.g.
The monochromatic intensity may be referred to as specific intensity,
while monochromatic flux may be called flux density, especially in
radio astronomy.
- The intensity is defined as the amount of energy transmitted through
a unit surface element per unit time per unit frequency (or
wavelength) into a unit solid angle in the direction (
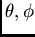 ),
where
),
where 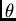 is the angle away from the normal to the surface
element, and
is the angle away from the normal to the surface
element, and 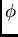 the azimuthal angle. The flux is the amount of
energy passing through a unit surface element in all directions,
defined by
the azimuthal angle. The flux is the amount of
energy passing through a unit surface element in all directions,
defined by
where 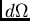 is the solid angle element, and the integration is over the
entire solid angle.
is the solid angle element, and the integration is over the
entire solid angle.
The luminosity is the intrinsic
energy emitted by the source per second.
Thus we can also consider it as the power. For an isotropically
emitting source,
where 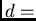 distance to source.
distance to source.
- What do we measure for sources? For unresolved sources, we measure
the flux, usually over some bandpass or wavelength interval, for resolved
sources we can directly measure their intensity distribution on the sky.
Only if we know the distance to a source, can we calculate the
luminosity of that source.
- Questions: how do the three quantities, L, I, and F depend
on distance to the source? What are the units of these three
quantities? (Note: there are many variations and you should make sure
you understand what is adopted by someone presenting data). There
is also no concensus between disciplines in the terminology,
so while astronomers are reasonably consistent in
the use of these terms, you may run into things like radiant flux,
irradiance, radiance, spectral intensity, and others, which are all
related but not exactly equal to intensity or flux.
To what quantity is apparent magnitude for a star related? To what
quantity the absolute magnitude?
- Light, by quantum mechanics, is photons, has characteristics
of both waves and particles. Wavelength/frequency corresponds to
energy:
- electromagnetic spectrum: gamma rays - X rays - UV - optical - IR -
mm - radio
- from astronomical sources, much astronomy is done by measuring
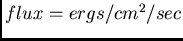 Other general branch is study of spatial distribution, i.e. astrometry,
morphology.
Other general branch is study of spatial distribution, i.e. astrometry,
morphology.
- for most sources, flux is a function of wavelength, so we actually
are often interested in estimates of the monochromatic flux, or
flux density = flux / unit wavelength.
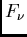 : flux per unit frequency.
: flux per unit frequency.
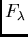 : flux per unit wavelength.
: flux per unit wavelength.
- Terminology of flux measurements:
- photometry (broad-band flux measurement),
- spectroscopy (relative measurement of fluxes at different wavelengths),
- spectrophotometry (absolute measurement of fluxes at different wavelengths).
- Generally, we measure flux, not flux density, though for narrow
band and spectroscopy they're almost equivalent. Also, with most
detectors, we measure photon flux (photon counting devices),
rather than energy flux (bolometers). The photon flux is given by
Magnitudes and the count equation
In astronomy, however, magnitudes are often used instead of
fluxes:
The flux density for astronomical objects may be specified by a
monochromatic magnitude:
where the coefficient of proportionality, 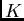 ,
depends on the definition of photometric system. In the STMAG system,
,
depends on the definition of photometric system. In the STMAG system,
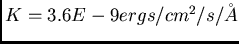 , which is the flux of Vega at 5500Å.
Alternatively,
we can write
, which is the flux of Vega at 5500Å.
Alternatively,
we can write
In the ABNU system,
we have
or
Related, but slightly different, are integrated magnitude systems;
the STMAG and ABMAG integrated systems are defined relative to sources of
constant 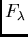 and
and 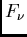 systems, respectively.
systems, respectively.
The standard UBVRI broadband photometric system, as well as many
other magnitude systems, however, are not defined for a constant 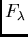 or
or 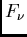 spectrum; rather, they are defined relative to the spectrum
of an A0V star. Most systems are defined (or at least were originally)
to have the magnitude of Vega be zero in all bandpasses.
spectrum; rather, they are defined relative to the spectrum
of an A0V star. Most systems are defined (or at least were originally)
to have the magnitude of Vega be zero in all bandpasses.
For the broadband UBVRI system, we have
Here is a plot
to demonstrate the
difference between the different systems.
Given a magnitude of an object in the desired band and absolute
spectrophotometry of Vega (Hayes 1985, Calibration of Fundamental Stellar
Quantities, IAU Sym 111), one can estimate the flux. Alternatively,
if one is given just the V magnitude of an object, a spectral energy
distribution (SED), and the filter profiles (Bessell 1990, PASP 102, 1181),
one can compute the integral of the SED over the V bandpass, determine
the scaling by comparing with the integral of the Vega spectrum over
the same bandpass, then use the normalized SED to compute the flux in
any desired bandpass. Some possibly useful references for SEDs are:
Bruzual, Persson, Gunn, & Stryker; Hunter, Christian, & Jacoby; Kurucz).
The photon flux from the source is not exactly what you measure.
To get the number of photons that you count in an observation, you
need to take into account the area of your photon collector (telescope),
photon losses and gains from the Earth's atmosphere, and the efficiency
of your collection/detection apparatus. Generally, the astronomical signal
can be written
where 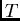 is the telescope collecting area,
is the telescope collecting area, 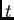 is the integration time,
is the integration time,
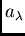 is the atmospheric transmission (next lecture) and
is the atmospheric transmission (next lecture) and
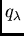 is the system efficiency.
is the system efficiency.
Usually, however, one doesn't use this information to go backward from S to
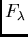 because it is very difficult to measure all of the terms precisely.
Instead, most observations are performed differentially to a set of standard stars, which themselves have been (usually painfully) calibrated.
We'll discuss this process in more depth later.
because it is very difficult to measure all of the terms precisely.
Instead, most observations are performed differentially to a set of standard stars, which themselves have been (usually painfully) calibrated.
We'll discuss this process in more depth later.
The count equation is used, however, very commonly, for computing the
approximate number of photons you will receive from a given source in
a given amount of time for a given observational setup. This number is
critical to know in order to estimate your expected errors and exposure
times in observing proposals, observing runs, etc. Understanding errors in
absolutely critical in all sciences, and maybe even more so in astronomy,
where objects are faint, photons are scarce, and errors are not at all
insignificant.
Errors in photon rates
For a given rate of emitted photons, there's a probability function which
gives the number of photons we detect, even assuming 100% detection
efficiency, because of statistical uncertainties. In addition,
there may also be instrumental uncertainties. Consequently, we
now turn to the concepts of probability distributions, with particular
interest in the distribution which applies to the detection of photons.
Distributions and characteristics thereof
- concept of a distribution : define
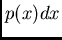 as probability of
event occuring in
as probability of
event occuring in 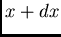 :
:
Some definitions relating to values which characterize a distribution:
median : mid-point value.
mode : most probable value
Note that the geometric interpretation of above quantities depends on
the nature of the distribution; although we all carry around the picture of
the mean and the variance for a Gaussian distribution, these pictures are
not applicable to other distributions.
Also, note that there is a difference between the sample mean,
variance, etc. and the population quantities. The latter apply
to the true distribution, while the former are estimates of the latter
from some finite sample of the population. The sample quantities are
derived from:
The sample mean and variance approach true mean and variance as N approaches
infinity.
Now we consider what distribution is appropriate for the detection
of photons. The photon distribution comes from the binomial
distribution, which gives the probability of observing the number,
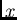 , of some possible event, given a total number of events
, of some possible event, given a total number of events 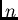 , and
the probability of observing the particular event (among all other
possibilities) in any single event,
, and
the probability of observing the particular event (among all other
possibilities) in any single event, 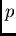 :
:
For the binomial distribution, one can derive:
In the case of detecting photons, 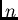 is the total number of photons
emitted, and
is the total number of photons
emitted, and 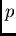 is the probability of detecting a single photon out out
of the total emitted. We don't know either of these numbers! However,
we do know that
is the probability of detecting a single photon out out
of the total emitted. We don't know either of these numbers! However,
we do know that  and we know, or at least we can estimate,
the mean number detected:
and we know, or at least we can estimate,
the mean number detected:
.
In this limit, the binomial distribution asymtotically approaches
the Poisson distribution:
From the expressions for the binomial distribution in this limit,
the mean of the distribution is 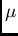 , and the variance is
, and the variance is
This is an important result.
Note that the Poisson distribution is generally the appropriate distribution
not only for counting photons, but for any sort of counting experiment.
What does the Poisson distribution look like?
Plots
for
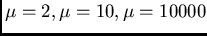 .
Note, for large
.
Note, for large 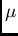 , the Poisson distribution is well-approximated around
the peak by a Gaussian, or normal distribution:
, the Poisson distribution is well-approximated around
the peak by a Gaussian, or normal distribution:
This is important because it allows us to use ``simple'' least squares
techniques to fit observational data, because these generally assume
normally distributed data. However, beware that in the tails of the
distribution, the Poisson distribution can differ significantly from a
Gaussian distribution.
The normal distribution is also important because many physical variables
seem to be distributed accordingly. This may not be an accident because
of the central limit theorem: if a quantity depends on a number of
independent random variables with ANY distribution, the quantity itself
will be distributed normally. (see statistics texts).
Importance of error distribution analysis
You need to understand the expected errors in your observations in
order to:
- predict the amount of observing time you'll need to get
errors as small as you need them to do your science,
- answer the question: is observed data consistent with expected errors?
If the answer is no, they you know you've either learned some
astrophysics or you don't understand something about your observations.
This is especially important in astronomy where objects are faint and
many projects are pushing down into the noise as far as possible.
Really we can usually only answer this probabilistically. Generally,
tests compute the probability that the observations are consistent with the
expected distribution (the null hypothesis). You can then look to see
if this probability is low, and if so, you can reject the null hypothesis.
Confidence levels
For example, say we want to know whether some single point is consistent
with expectations, e.g., we see a bright point in multiple measurements
of a star, and want to know whether the star flared. Say we have a time
sequence with known mean and variance, and we obtain a new point, and
want to know whether it is consistent with known distribution.
In the limit where the observed distribution is approximately Gaussian,
we can calculate the error function, which is the integral of a
gaussian. From this, we can determine the probability of obtaining some
point given the known distribution.
Some simple guidelines to keep in mind (the actual situation often
requires more sophisticated statistical tests) follow. First, for
Gaussian distributions, you can calculate that 68% of the points
should fall within plus or minus one sigma from the mean, and 95.3%
between plus or minus two sigma from the mean. Thus, if you have a
time line of photon fluxes for a star, with N observed points, and a
photon noise 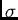 on each measurement, you can test whether the
number of points deviating more than
on each measurement, you can test whether the
number of points deviating more than 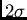 from the mean is much
larger than expected. To decide whether any single point is really
significantly different, you would want to use a
from the mean is much
larger than expected. To decide whether any single point is really
significantly different, you would want to use a 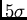 rather than
a
rather than
a 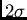 criterion. The
criterion. The 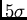 has much higher level of
significance of course. On the other hand, if you have far more points
in the range
has much higher level of
significance of course. On the other hand, if you have far more points
in the range  brighter or fainter than you would expect,
you may also have a significant detection of intensity variations
(provided you really understand your uncertainties on the
measurements!).
brighter or fainter than you would expect,
you may also have a significant detection of intensity variations
(provided you really understand your uncertainties on the
measurements!).
Noise equation: how do we predict expected errors?
Given an estimate the number of photons expected from an object in
an observation, we then can calulate the signal-to-noise ratio:
which gives the inverse of
the predicted fractional error (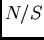 ).
).
Consider an object with photon flux (per unit area and time), 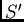 ,
leading to a signal,
,
leading to a signal,
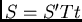 where
where 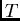 is the telescope area and
is the telescope area and
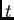 is the exposure time. In the simplest case, the only noise source
is Poisson statistics from the source, in which case:
is the exposure time. In the simplest case, the only noise source
is Poisson statistics from the source, in which case:
In other words, the S/N increases as the square root of the object
brightness, telescope area, efficiency, or exposure time.
A more realistic case includes the noise contributed from Poisson statistics
of background light (next lecture), 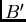 ,
which has units of flux per area on the sky (also usually given in magnitudes).
,
which has units of flux per area on the sky (also usually given in magnitudes).
The amount of background in our measurement depends on how we
choose to make the measurement (how much sky area we observe).
Say we just use an aperture with area, 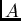 .
.
The total number of photons observed, 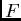 , is
, is
The variance of the total flux, from Poisson statistics, is:
since the variances add for object+background.
To get the desired signal, we will need to measure separately the total signal
and the background signal to estimate:
where 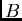 is some estimate we have obtained of the background level multiplied
by the area A (
is some estimate we have obtained of the background level multiplied
by the area A (
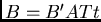 ).
The noise in the measurement is
).
The noise in the measurement is
where the approximation is accurate
if the background is determined to high accuracy.
This leads to a common form of the noise equation:
In the signal-limited
case,
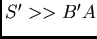 , we get
, we get
In the background limited case,
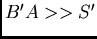 , and
, and
S/N drops faster when you're background limited. This illustrates
the importance of dark-sky sites, and also the importance of good
image quality.
Consider two telescopes of collecting area, 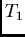 and
and 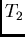 . If we
observe for the same exposure time on each and want to know how much
fainter we can see with the larger telescope at a given S/N, we
find:
. If we
observe for the same exposure time on each and want to know how much
fainter we can see with the larger telescope at a given S/N, we
find:
for the signal-limited case, but
for the background-limited case.
Instrumental noise
In addition to the errors from Poisson statistics (statistical noise),
there may be additional terms from instrumental errors. A prime example
of this using CCD detectors is readout noise, which is additive noise
(with zero mean) which comes from the detector, and is independent of
signal level. For a detector whose readout noise is characterized by
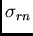 ,
,
if a measurement is made in a single pixel. If an object is spread over
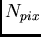 pixels, then
pixels, then
For large 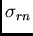 , the behavior is the same as the background
limited case. This makes it clear that if you have readout noise, image
quality (and/or proper optics to keep an object from covering too many pixels)
is important for maximizing S/N. It is also clear that it
is critical to have minimum read-noise for low background applications
(e.g., spectroscopy).
, the behavior is the same as the background
limited case. This makes it clear that if you have readout noise, image
quality (and/or proper optics to keep an object from covering too many pixels)
is important for maximizing S/N. It is also clear that it
is critical to have minimum read-noise for low background applications
(e.g., spectroscopy).
There are other possible additional terms in the noise equation,
arising from things like dark current, digitization noise, errors in
sky determination, errors from photometric technique, etc.; we'll discuss
some of these later on.
Error propagation
Consider what happens if you have several known quantities
with known error distributions and you combine these into some
new quantity: we wish to know what the error is in the new quantity.
The question is what is 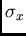 if we know
if we know 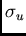 ,
, 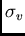 , etc.?
, etc.?
As long as errors are small:
The last term is the covariance, which
relates to whether errors are /it correlated.
If errors are uncorrelated, then
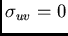 because there's
equal chance of getting opposite signs on
because there's
equal chance of getting opposite signs on 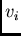 for any given
for any given 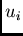 .
.
Examples:
- addition/subtraction:
- multiplication/division:
- logs:
Distribution of resultant errors
When propagating errors, even though you can calculate
the variances in the new variables, the distribution of errors in the
new variables is not, in general, the same as the distribution of errors in
the original variables, e.g. if errors in individual variables
are normally distributed, errors in output variable is not
necessarily.
When two variables are added, however, the output is normally distributed.
Determining sample parameters: averaging measurements
We've covered errors in single measurements. Next we turn to
averaging measurements. say we have multiple observations and want the
best estimate of the mean and variance of the population, e.g. multiple
measurements of stellar brightness. Here we'll define the best estimate
of the mean as the value which maximizes the likelihood that our estimate
equals the true parent population mean.
For equal errors, this estimate just gives our normal expression for
the sample mean:
Using error propagation, the estimate of the error in the sample mean
is given by:
But what if errors on each observation
aren't equal, say for example we have observations
made with several different exposure times? Then we determine the
sample mean using a:
and the estimated error in this value is given by:
where the 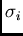 's are individual weights.
's are individual weights.
This is fine, but how do we go about choosing the weights, 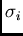 ?
We know we can estimate
?
We know we can estimate 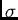 using Poisson statistics for a
given count rate, but remember that this is a sample variance (based on
a single observation!) not the true variance. This can lead to biases.
using Poisson statistics for a
given count rate, but remember that this is a sample variance (based on
a single observation!) not the true variance. This can lead to biases.
Consider observations of a star made on three nights, with measurements
of 40, 50, and 60 photons. It's clear that the mean observation is
50 photons. However, beware of the being trapped by your error estimates. From each observation alone, you would estimate errors of
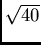 ,
, 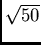 , and
, and 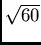 . If you plug these error
estimates into a computation of the weighted mean, you'll get a mean
rate of 48.64!
. If you plug these error
estimates into a computation of the weighted mean, you'll get a mean
rate of 48.64!
Using the individual estimates of the variances, we'll bias values to
lower rates, since these will have estimated higher S/N.
Note that it's pretty obvious from this example that you should just
weight all observations equally. However, note that this certainly isn't
always the right thing to do. For example, consider the situation in
which you have three exposures of different exposure times. Here you
clearly want to give the longer exposures higher weight. In this case,
you again don't want to use the individual error estimates or you'll
introduce a bias. There is a simple solution here also: just weight the
observations by the exposure time. This works fine for Poisson errors
(variances proportional to count rate), but not if there are instrumental
errors as well which don't scale with exposure time. For example,
the presence of read noise can have this effect. With read noise, the
longer exposures should be weighted even higher than expected for the
exposure time ratios. The only way to properly average measurements in
this case is to estimate a sample mean, then use this value scaled to
the appropriate exposure times as the input for the Poisson errors.
Can you split exposures?
When observing, one must consider the question of how long individual
exposures should
be. There are several reasons why one might imagine that it is nicer to
have a sequence of shorter exposures rather than one single longer exposure
(e.g., tracking, monitoring of photometric conditions, cosmic ray rejection),
so we need to consider whether doing this results in poorer S/N.
Consider the object with photon flux 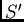 , background surface brightness
, background surface brightness
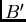 ,
and detector with readout noise
,
and detector with readout noise 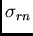 . A single short
exposure of time
. A single short
exposure of time 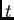 has a variance:
has a variance:
If 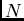 exposures are summed, the resulting variance will be
exposures are summed, the resulting variance will be
If a single long exposure of length 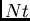 is taken, we get
is taken, we get
The ratio of the noises, or the inverse ratio of the 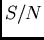 (since the total signal measured is the same in both cases), is
(since the total signal measured is the same in both cases), is
In the signal- or background-limited regimes, exposures can be added
with no loss of
S/N. However, if readout noise is significant, then splitting exposures
leads to reduced S/N.
Random errors vs systematic errors
So far, we've been discussing random errors. There is an additional,
usually more troublesome, type of errors known as systematic errors.
These don't occur randomly but rather are correlated with some, possibly
unknown, variable relating to your observations.
EXAMPLE : flat fielding
EXAMPLE : WFPC2 CTE
Note also that in some cases, systematic errors can masquerade as random
errors in your test observations, but actually be systematic in your
science observations
EXAMPLE: flat fielding, subpixel QE variations.
Note that error analysis from expected random errors may be the only clue
you get to discovering systematic errors. To discover systematic errors,
plot residuals vs. everything!


Next: Intermezzo on Fourier Transforms,
Up: AY535 class notes
Previous: Class introduction
Rene Walterbos
2003-04-14
![]() is the solid angle element, and the integration is over the
entire solid angle.
is the solid angle element, and the integration is over the
entire solid angle.
![]() distance to source.
distance to source.