Aberration compensation and different telescope types

Using the techniques above, we can write expressions for the system aberrations as a function of the surface figures (and field angles). If we give ourselves the freedom to choose surface figures, we can eliminate one (or more) aberrations. For example, if we set the primary to be a parabola ($K_1 = -1$), we can use the aberration relations to determine $K_2$ such that spherical aberration is zero; this will give us perfect images on-axis. We find that:

$$K_2 = -\left({(m+1)\over(m-1)}\right)^2 + {m^3\over k (m-1)^3)}(K_1+1)$$

satisfies this criterion. This type of telescope is called a classical telescope. Using the aberration relations, we can determine the amount of astigmatism and coma for such telescopes, and we find that coma gives significantly larger aberrations than astigmatism.

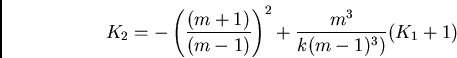
If we allow ourselves the freedom to choose both $K_1$ and $K_2$, we can eliminate both spherical aberration and coma. Designs of this sort are called aplanatic. The relevant expression, in terms of the magnification and back focal distance (we could use the relations discussed earlier to present these in terms of other paraxial parameters), is:

$$K_1 = -1 - {2(1+\beta)\over m^2(m-\beta)}$$

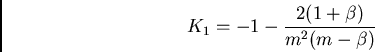
We can only eliminate two aberrations with two mirrors, so even this telescope will be left with astigmatism.

There are two different classes of two-mirror telescopes: Cassegrain telescopes and Gregorian telescopes. For the classical telescope with a parabolic primary, the Cassegrain secondary is hyperbolic, whereas for a Gregorian it is ellipsoidal (because of the appropriate conic sections derived above for convex and concave mirrors with finite conjugates). For the aplanatic design, the Cassegrain telescope has two hyperbolic mirrors, while the Gregorian telescope has two ellipsoidal mirrors. An aplanatic Cassegrain telescope is called a Ritchey-Chretien telescope.

The following table gives some characteristics of ``typical'' telescopes. Aberrations are given at a field angle of 18 arc-mm in units of arc-seconds. Coma is given in terms of tangential coma.

Characteristics of Two-Mirror Telescopes

Parameter	CC	CG	RC	AG
m	4.00	-4.00	4.00	-4.00
k	0.25	-0.417	0.25	-0.417
1 - k	0.75	1.417	0.75	1.417
mk	1.000	1.667	1.000	1.667
ATC	2.03	2.03	0.00	0.00
AAS	0.92	0.92	1.03	0.80
ADI	0.079	0.061	0.075	0.056
$\kappa_m R_1$	7.25	-4.75	7.625	-5.175
$\kappa_p R_1$	4.00	-8.00	4.00	-8.00

The image quality is clearly better for the aplanatic designs than for the classical designs, as expected because coma dominates off-axis in the classical design. In the aplanatic design, the Gregorian is slightly better. However, when considerations other than just optical quality are considered, the Cassegrain usually is favored: for the same primary mirror, the Cassegrain is considerably shorter and thus it is less costly to build an enclosure and telescope structure. To keep the physical length the same, the Gregorian would have to have a faster primary mirror, which are more difficult (i.e. costly) to fabricate, and which will result in a greater sensitivity to alignment errors. Both types of telescopes have a curved focal plane.