Aberrations: general description and low-order abberrations

Now consider what happens for surfaces that are not perfect, e.g. for the cases considered above for field angle$\not=$0 (since only a sphere is symmetric for all field angles), or for field angle 0 for a conic surface which doesn't give a perfect image?

You get aberrations; the light from all locations in aperture does not land at any common point.

One can consider aberrations in either of two ways:

1. aberrations arise from all rays not landing at a common point,
2. aberrations arise because wavefront deviates from a spherical wavefront.

These two descriptions are equivalent. For the former, one can talk about the transverse aberrations, which give the distance by which the rays miss the paraxial focus, or the angular aberration, which is the angle by which the rays deviate from the perfect ray which will hit paraxial focus. For the latter, one discusses the wavefront error, i.e., the deviation of the wavefront from a spherical wavefront as a function of location in the exit pupil.

First, consider where rays land as f(z). We can derive the effective focal length as f(z) for an arbitrary conic section for field angle=0:

$$z_0 = \rho / \tan (2 \phi) = \rho (1-(\tan \phi)^2) / ( 2 \tan \phi)$$

$$\tan \phi = dz / d\rho$$

from conic equation:

$$\rho^2 - 2 R z + (1+K) z^2 = 0$$

$$z={R\over(1+K)}\left[1-\left(1-{\rho^2\over R^2}(1+K)\right)^{1/2}\right]$$

$$z\approx {\rho^2\over 2R} + (1+K){\rho^4\over 8 R^3} + (1+K)^2 {\rho^6\over 16 R^5} + \dots$$

$$dz/d\rho = \rho / (R - (1-K)z)$$

$$z_0 = {\rho \over 2} \left[{ R - (1+K)z\over\rho} - {\rho\over R-(1+K)z } \right]$$

$$f_e = z + z_0$$

$$f_e = {R\over 2} + {(1-K) z\over 2} - {\rho^2\over 2 (R-(1+K) z}$$

$$f_e = {R\over 2} - (1+K) {\rho^2\over 4 R} - (1+K)(3+K) {\rho^4\over 16 R^3} - ...$$

$$\Delta f = f_e - {R\over 2}$$

Note that $f_e$ is independent of $z$ only for $K=-1$, a parabola. Also note that $\Delta f$ is symmetric with respect to $\rho$.

We define spherical aberration as the aberration resulting from $K\ne -1$. It is an aberration which is present on axis as seen here. Spherical aberration is symmetric in the pupil. There is no location in space where all rays focus at a point. In fact, the behavior as a function of focal position is not symmetric. One can define several criteria for where the ``best focus'' might be, leading to the terminology paraxial focus, marginal focus, diffraction focus, and the circle of least confusion.

The asymmetric nature of spherical aberration as a function of focal position distinguishes it from other aberrations and is a useful diagnostic for whether a system has this aberration. This is shown in this figure which shows a sequence of images at different focal positions in the presence of spherical aberration. We define transverse spherical aberration (TSA) as the image size at paraxial focus. This is not the location of the minimum image size.

$${TSA \over \Delta f} = {\rho \over (f - z(\rho))}$$

$$TSA = - (1+K) {\rho^3 \over 2 R^2} - 3(1+K)(3+K) {\rho^5\over 8 R^4} + ...$$

We can also consider aberration as the difference between our wavefront and a spherical wavefront, which in this case is given by a parabolic surface.

$$\Delta z = z_{parabola} - z(K) = - {\rho^4 \over 8 R^3} (1+K) + \dots$$

The difference in angle between the ``perfect'' ray from the parabola and the actual ray is called the angular aberration, in this case angular spherical aberration, or ASA.

$$ASA = 2 (\phi_p - \phi) \approx {d\over d\rho} (2\Delta z) \approx -(1+K) {\rho^3 \over R^3}$$

where $2\Delta z$ gives the optical path difference between the two rays.

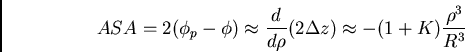
This is simply related to the transverse aberration:

$$TSA = {R\over 2} ASA$$

This result can be generalized to any sort of aberration: the angular and transverse aberrations can be determined from the optical path difference between a given ray and that of a spherical wavefront. The relations are given by:

$$\mathrm{angular aberration} = d/d\rho (2 \Delta z)$$

$$\mathrm{transverse aberration} = s' d/d\rho (2 \Delta z)$$

If the aberrations are not symmetric in the pupil, then we could define angular and transverse $x$ and $y$ aberrations separation by taking derivatives with respect to $x$ or $y$ instead of $\rho$.

We can describe deviations from a spherical wavefront generally. Since all we care about are optical path differences, we write an expression for the optical path difference between an arbitrary ray and the chief ray, and in doing this, we can also include the possibility of an off-axis image, and get

$$OPD = OPL - OPL(chief ray)$$

$$OPD = A_0 y + A_1 y^2 + A_1' x^2 + A_2 y^3 + A_2' x^2 y + A_3 \rho^4$$

where we've kept terms only to fourth order and chosen our coordinate system such that the object lies in the y-z plane. The coefficients, $A$, depend on lots of things, such as ( $\theta, K, n, R, s, s'$).

Analytically, people generally restrict themselves to talking about third-order aberrations, which are fourth-order (in powers of $x,y,\rho, \mathrm{or} \theta$) in the optical path difference, because of the derivative we take to get transverse or angular aberrations. In the third-order limit, one finds that $A_2 = A_2'$, and $A_1 = - A_1'$. Working out the geometry, we find for a mirror that:

$$A_0 = 0$$

$$A_1 = {n\theta^2\over R}$$

$$A_2 = - {n\theta\over R^2} \left({m+1\over m-1}\right)$$

$$A_3 = {n\over 4 R^3}\left[K + \left({m+1\over m-1}\right)^2\right]$$

From the general expression, we can derive the angular or the transverse aberrations in either the x or y direction. Considering the aberrations in the y direction, we find:

$$AA_y = 2 A_1 y + A_2 (x^2 + 3y^2) + 4 A_3 y \rho^2$$

$$AA_x = 2 A_1 x + 2 A_2 xy + 4 A_3 x \rho^2$$

The first term is proportional to $\theta^2 y$ and is called astigmatism. The second term is proportional to $\theta (x^2 + 3y^2)$ and is called coma. The final term, proportional to $y\rho^2$ is spherical aberration, which we've already discussed (note for spherical, $AA_x = AA_y$ and in fact the AA in any direction is equal, hence the aberration is circularly symmetric).

Note that rays along the y-axis are called tangential rays, while rays along the x-axis are called sagittal rays.

For astigmatism, rays from opposite sides of the pupil focus in different locations relative to the paraxial rays. At the paraxial focus, we end up with a circular image. As you move away from this image location, you move towards the tangential focus in one direction and the sagittal focus in the other direction. At either of these locations, the astigmatic image looks like a line. Astigmatism goes as $\theta^2$, and consequently looks the same for opposite field angles. Astigmatism is characterized in the image plane by the transverse or angular astigmatism (TAS or AAS), which refer to the height of the marginal rays at the paraxial focus. Astigmatism is symmetric around zero field angle.

This figure shows the rays in the presence of astigmatism.
This figure shows the behavior of astigmatism as one passes through paraxial focus. For coma, rays from opposite sides of the pupil focus at the same location. However, the tangential rays focus at a different location than the sagittal rays, and neither of these focus at the paraxial focus. The net effect is to make an image that vaguely looks like a comet, hence the name coma. Coma goes as $\theta$, so the direction of the comet flips sign for opposite field angles. Coma is characterized by either the tangential or sagittal transverse/angular coma (TTC, TSC, ATC, ASC) which describe the height/angle of either the tangential or sagittal marginal rays at the paraxial focus: $TTC = 3 TSC$.

This figure shows the rays in the presence of coma.
This figure shows the behavior of coma as one passes through paraxial focus. In fact, there are two more third-order aberrations which we haven't yet discussed: distortion and field curvature. Neither affects image quality, only location (unless you are forced to use a flat image plane!). Distortion goes as $\theta^3$. The field curvatures can be derived from the aberration coefficients and the mirror parameters.

We can also determine the relevant coefficients for a surface with a displaced stop (Schroeder p 77), or for a surface with a decentered pupil (Schroeder p89-90); it's just more geometry and algebra. With all these realtions, we can determine the optical path differences for an entire system: for a multi-surface system, we just add the OPD's as we go from surface to surface. The final aberrations can be determined from the system OPD.