The origin of this mysterious force called gravity was the subject of intense debate. The true understanding (at least to the point of what is going on, but not why mass actually exerts a force called gravity---a very deep, and difficult subject) had to wait until Einstein's theory of General Relativity in 1916. But Newton's approach, that mathematics can be used to understand the Universe, was the true beginning of modern physics.

To understand a little about gravity, we need to discuss some new terms. First let's tackle "mass" and "weight". You are probably familiar with these two terms, but they have completely different meanings. In the English system, weight is measured in "pounds". In the metric system "mass" is measured in kilograms. You may have even seen the conversion 1 kg = 2.2 lbs. But this conversion only works at the Earth's surface. Why? Because mass is an intrinsic property of the object--whether a grain of sand, a rock, a human being, a car, a planet, etc. They all have a "mass" that is always the same number of kilograms, no matter where they are located. But an object's weight depends on where it is located. On the Earth's surface, an object with a mass of 100 kg has a weight of 220 lbs. But on the Moon, the weight of that object is only 36.5 lbs. On Jupiter (which has 318 times the Earth's mass) that weight would be 520 lbs! (To see what you would weigh on other worlds go here.)

So for an astronaut orbiting the Earth in the Space Shuttle, we talk about them being "weightless". But obviously, they have not lost any mass! Weight is what a bathroom scale reads, and it comes about through the gravity from the Earth's mass pulling on objects. We talk about the "acceleration" of gravity. You are familiar with the term acceleration---you hit the gas pedal ("accelerator") in your car and you go faster, and faster. 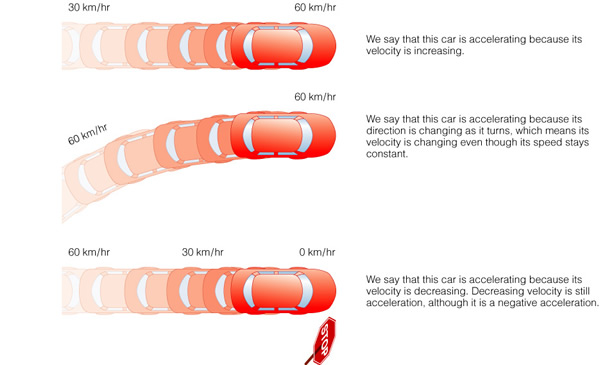An acceleration is the changing velocity of an object (also read section 4.1 to see the real definitions of "speed" and "velocity"--we will just consider them to be the same thing for our discussion here, but technically they are not quite the same thing). As shown in Figure 4.1, an object that is speeding up is accelerating--but so is a car going around a corner, or one that is slowing down, "decelerating". A car that is speeding up has a positive acceleration, one that is slowing has a negative acceleration.

So, how do we accelerate a car? We push on the gas, using more and more of our gasoline (energy!) to speed up. To decelerate we push on the brake---we are again using energy, but this time the brake heats up from the friction to dissipate the speed of the car. If you have ever pulled a heavy load, or descended down a very steep hill, you can smell your brakes when you try to slow down---the energy contained in your motion, the "momentum", has to be dissipated, and in slowing it is transfered to heat, and this creates a smell as the brake pads/shoes heat up.

Ok, now we know from experience that "what goes up, must come down". So, let's climb to the top of a tall building and drop a rock. What happens? Initially, for just an instant, the rock is not moving, but then it falls, and as it falls it speeds up---it is accelerating. Not only that, it is accelerating at a specific rate. This is shown in Fig 4.2:

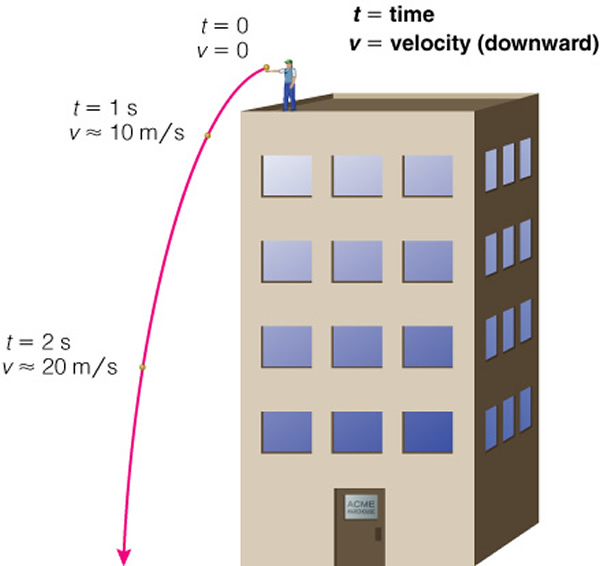
After one second (t = 1s), the rock is moving at a velocity of 10 m/s, after two seconds (t = 2 s) the rock is moving with a velocity of 20 m/s. We can write this as an equation: v = 10 x t. Using this equation, we know that if t = 4 s, then v = 40 m/s. Ok, so velocity is measured in meters per second (or kilometers per second, or kilometers per hour, or miles per hour, etc.). The "10" in our equation (which is actually 9.8) has to have the weird units of m/s² ("meters per second squared") to get the units on the equation to work out. This "10" is called the gravitational acceleration constant, abbreviated "g". So, in actuality, the equation is v = gt. And "g" depends on the local gravity. On Jupiter "g" is bigger, on the Moon "g" is smaller. On the Earth g = 9.8 m/s².

This gravitational constant also is what determines your weight! In fact, weight = mass x g. Let's be more general now, and revert to calling "g" the acceleration, abbreviated by "a". Now our equation becomes w = ma. And, calling weight the "force of gravity", abbreviated by "F", we get the equation F = ma. This is the second of Newton's laws that we listed above: force = mass x acceleration. A "Force" is something that tries to change the acceleration of a mass. When you jump up into the air (to dunk a basketball), the force of gravity changes your acceleration: you go up for a while all the time slowing, stop, then go back down, accelerating as you fall. This force of gravity is what keeps the planets orbiting around the Sun on elliptical orbits. But this is just part of the explanation (and it was Newton that developed and used the theory of gravity to explain Kepler's laws).

To understand why planets orbit the Sun (or why the moon orbits the Earth) we have to talk a little more about motion. Newton's first law states that "in the absence of a net force acting upon it, an object in motion moves with constant velocity". This is kind of hard to envision on the surface of the Earth. If we were to throw a baseball, it would go a little ways, but eventually crash into the surface of the Earth. Why? Because the Earth's gravity is a force that changes the motion of the baseball. But, if we could move into deep space and then throw our baseball, then without any nearby masses, it would move at a uniform velocity through space. But near a large mass, the path of the baseball is altered--it is curved.

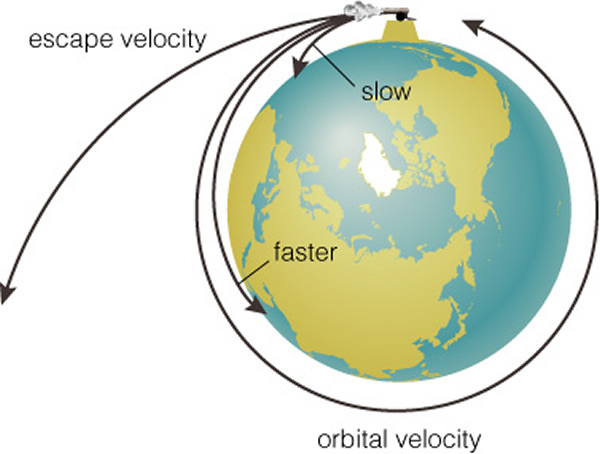
We have had to play a thought game to understand this motion---let's make some more mental leaps and imagine shooting a cannonball off a very tall mountain. This is shown in the figure, below. If we use a little bit of powder, and the ball comes out slowly, it will crash close to the mountain. Let's add more powder and blast it out at a higher velocity---the ball travels further. But Earth's gravity wins and the ball eventually crashes back to Earth. Now, what happens if we shoot the ball to a very high speed so much so that it doesn't crash back into the Earth. Is this possible? Yes, it is called orbital velocity! This is what rockets like the Space Shuttle do, they go fast enough to reach orbit. What is an orbit? Well it is the speed at which the cannonball (or spacecraft) is going where it "continuously falls around the Earth" without hitting it. The gravity of the Earth continually curves the motion of the ball, but at just the right rate so that the cannon ball never hits the Earth. Of course we could use so much explosive that the cannon ball is not captured by the Earth but blasts itself into deep space---just like we must do to launch a space probe to another planet. We call the velocity where the object permanently leaves the Earth, the "escape velocity" (this is a very high speed: 40,000 km/hr!):

So, how can we understand this curvature thing? Let's look at a simple example, a ball attached to a string that is spun around our head, as in Figure 4.6:

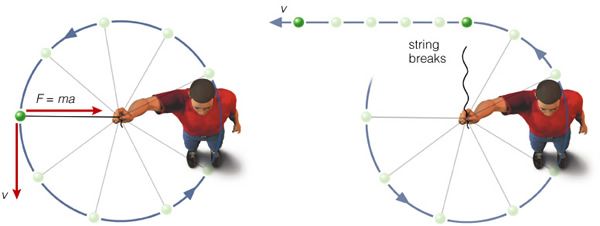
As long as the string holds, the ball will circle our head---but if it breaks, the ball flies off! What is the force acting on the ball? Well it is the string! The string is the force acting to keep the ball in motion around our head (though we supply the energy). If we could keep spinning the ball faster and faster it would eventually break the string--it would "escape". This is just like gravity---gravity is the invisible string that keeps the ball (or satellite) orbiting the Earth.

We can now expand upon this demonstration to understand Kepler's third law. If we suddenly shorten the string, what happens? The ball goes around faster! If we lengthen the string, the ball goes around more slowly--just like planets. Mercury is close to the Sun, it's "string" is short (in reality the force of gravity of the Sun is larger), so it has to go around fast (to balance the larger gravitational force) or else it will crash into the Sun (Mercury's orbital period is only 88 days). Jupiter is five times further from the Sun then the Earth, its string is long, so it moves slowly--it takes Jupiter more than 11 years to go around the Sun. Kepler's third law, P² ∝ a³, says the longer the string ("a") the slower the planet moves and the longer the orbital period ("P").

It is the force of gravity that keeps planets and comets in orbit around the Sun, and the various moons in orbit around their planets. Newton realized that to explain Kepler's third law, the "force of gravity", that is the force that attracts two bodies with "mass", must be directly proportional to their masses, but inversely proportional to the the square of the separation between them:

The "G" in this equation is the "gravitational constant" that makes the equation work. It is something that must be experimentally measured. Here is a figure showing the geometry of gravitational attraction:

Using his understanding of how gravity works, Newton figured out how to turn Kepler's "∝" (P² ∝ a³) into an equals sign:

G is the fundamental gravitational constant: G = 6.67 X 10^-11 that must be measured in the lab experimentally.

Now you can see how we measure the mass of a star or planet--we figure out the semi-major axis "a" (the mean distance) and the orbital period. Let's work an example. Let's use Venus to measure the mass of the Sun. Venus orbits at a distance of a= 0.72 AU = 108,200,000 km, its orbital period is 225 days. We need to put these quantities into meters and seconds. a = 108,200,000 km X 1,000 m/km = 1.08 x 10¹¹ m. P = 225 X 24 X 3600 = 1.94 X 10⁷ s. Let's rewrite that equation to solve for (M_p+M_sun):

Since the Sun's mass is many hundreds of times that of Venus, we just ignore Venus' mass, and we have:

This is essentially how we measure the masses of planets and of stars. We figure out the orbital period and how fast the two objects are moving, and we can get the mass. We use the Doppler effect to measure velocity of the two stars, and the repeating period of the spectral lines gives us the orbital period. Assuming a circular orbit, you then know that 2πa = circumference, and that the star travels this in a time "t", the orbital period. Using some substitution (which we will not do), you can then figure out the masses.

Ok, so let's use some more of this physics. With some simple mathematics (well, calculus) and an understanding of Newton's laws, one can now derive the escape velocity mentioned above. The escape velocity is:

To leave a massive object, we must attain this velocity. The "M" in this equation is the mass of the object, G is the fundamental gravitational constant: G = 6.67 X 10^-11 m³ kg^-1s^-2, "r" is the radius at which you are launching from. Let's work the example for the Earth (note with G in the units above, we have to convert everything to meters and kilograms!). We are going to want to escape the Earth's surface. The surface of the Earth is at a radius (Earth's radius!) of r = 6378 km = 6.38 X 10⁶ m. The mass in this equation is the Earth's mass: 5.9 X 10²⁴ kg. Let's first square both sides to get rid of the square root:

Plugging in the numbers:

Taking the square root of both sides:

This is the speed at which you must shoot an object for it to leave the Earth's surface, and never come back. Of course, if you have a rocket, you can continually apply thrust, and because you are moving away, "r" gets bigger, and thus V_esc goes down. We cannot launch rockets at the escape speed, but they have motors that burn for a long time, and thus can get to the escape speed eventually.

Ok, now let's go back to black holes. We said "no light escapes", so the escape speed for a black hole has to be the speed of light: c = 300,000 km/s, or 3 X 10⁸ m/s. Let's redo the calculation, but leave it in terms of M/r momentarily:

How big is such an object? First we must estimate its mass, let's choose two times the mass of the Sun: 2 X 2 X 10³⁰ kg. So now we have:

The smallest black holes that we know about generally have four or five times the mass of the Sun. The mass of the typical neutron star is 1.4 times that of the Sun, so that leads to a radius of 4.2 km or, as we said last week, 8 km in diameter!

There is a lot more to gravity that we do not have time to discuss, we are glossing-over most of the subject here. To get a full flavor for this subject, read Chapter 4 in its entirety. To get more requires you to take a physics class (for a simple tutorial, go here). Note that Newton's laws work pretty well for navigating through the solar system. But when you get very close to the Sun, or to other large bodies (such as black holes), all sorts of weird affects reveal themselves. Einstein showed that Newton's laws were not the correct description of gravity, and they only worked fairly well for (and near) "low mass" objects like planets. Objects of higher masses and densities (stars and remnants of stars) require Einsten's theory of general relativity where the gravitational force is actually due to the curvature of empty space! This is a subject beyond our abilities to discuss in this class, but a site like Wikipedia can supply additional details. It is interesting to note that without taking the effects of general relativity into effect, the GPS system that we use for navigation would not work. To read more about this, go here.

Now that we know about gravity, we can gain a deeper understanding of how stars operate. Last week we said the "force of gravity is balanced by the energy generation rate" to keep a star stable. The energy generation rate is simply the star's luminosity "L". The force exerted by the luminosity on a gas molecule at the surface of a star like the Sun is actully somewhat complicated due to how this light must be absorbed:

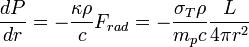
"F_rad" is the "force of radiation". It is related to luminosity by this equation. All of that junk in front of "L/4πr²" is just a number that describes hydrogen absorption, so being just a number, we will call it "A" (the ρ in this equation should be a "N_elec/cm³", and is just a number). So now we set up what is called the equation of hydrostatic equilibrium:

See what we are doing? We balance the force of gravity with the force caused by the energy generation rate. Note both have an r² in the denominator so those cancel, and after some re-arranging we get:

We roll all of the constants (G, 4π, m_hyd, and A) into a new constant "B", and we get:

The bigger the mass, the more luminosity that must be generated to keep the star stable. The number B is pretty small when you work it out, B = 1/30,000 = 0.00003, so that is why a star with 60 solar masses has to have a luminosity near 1.8 million times that of the Sun to be in balance.

Ok, now let's look at a red giant, a phase in a star's life where it has grown to enormous proportions. First, how big is it? In this week's homework you have seen the equation we need to estimate the radius: L = 4πR²sT⁴. The temperature of a red giant is about 4000 K, the luminosity is about 1,000 times that of the Sun. So we use this equation just like in the homework, we ratio it relative to the same equation for the Sun:

By ratioing the equations we get rid of all of the constants (4πs), solving for R, and plugging in the numbers we get:

In that last step we took the square root of both sides, and rearranged the R's. Now we have a radius, we can examine the force of gravity at the surface of the Sun, vs that at the surface of a red giant that has the mass of the Sun (i.e., the "future" Sun). We do this again by ratioing equations, this time we use the gravity equation (the little "m" in the gravity equation will be the mass of a hydrogen atom in the photosphere):

Though this equation looks messy, remember M_RG = M_Sun, and thus we cancel out the M's and the m's (also the "G", which we did not put in there cancels), leaving us:

We just calculated that R_RG= 66.5 R_Sun, so this equation is simply:

The force of gravity at the surface of the red giant is a tiny fraction of the force of gravity at the surface of the Sun! Thus, the gas can easily achieve escape velocity. The escape velocity at the Sun's surface is 617.5 km/s, but at the surface of the red giant, the escape velocity is only 75 km/s (you can verify this for yourself using the escape velocity equation above). The mean velocity of hydrogen atoms in a 4000 K gas is about 10 km/s. But when we say "mean" velocity we are talking about a function that sort of resembles a bell curve (go here for more). A tiny fraction of the atoms in the gas are going seven or eight times faster than this, and thus they easily escape the surface, and a red giant loses mass to a "wind". Note that in the later stages of evolution, the red giant can grow even larger, and have a higher luminosity. At these times, the escape velocity becomes almost equal to the mean velocity of the gas, and much of the atmosphere can be shed---creating a planetary nebula and a hot bare core: the white dwarf.

As we have described in previous classes, there are a lot of "inverse square laws" in physics. That is a 1/r². You've seen them in the derivations above. Why is that? Those terms are due to the fact that these forces radiate into space in all directions, penetrating a spherical surface. The area of a sphere is 4πr². Thus, if you double the radius of a sphere, the area of the sphere quadruples:

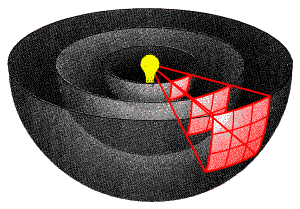
If you triple the radius the area increases by a factor of 9. The force of gravity is one of these laws---the force is concentrated at the center of an object like the Earth or Sun. As you go further from the source of gravity, the force is diluted, and the dilution factor is exactly 1/4πr².