In the last class we talked about Olbers' and Newton's paradoxes. Today we will find out how they were resolved. During the first part of the 20th century, astronomers finally began to obtain spectra of galaxies to investigate their nature. Remember that a spectrum requires you to break up the light into its various colors. For most applications, astronomers use spectrographs that have "resolutions of 1,000" or more. What this means is that the light that forms an optical image of a star on a photograph or other detector is broken up into 1,000 individual pieces--an image of the star at many different wavelengths. We call this a spectrum. Here is the spectrum of the Sun (see the notes for Class #13):

The dark lines in this spectrum correspond to electron transitions in various different elements. Remember that each element has a unique spectrum, and will have absorption or emission lines at unique positions, or wavelengths in the spectrum. Here is the spectrum of hydrogen:

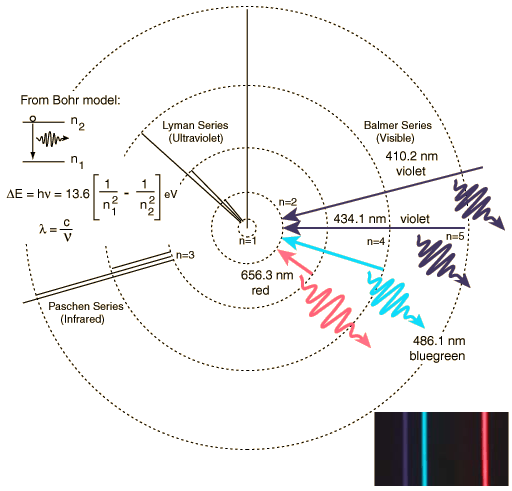
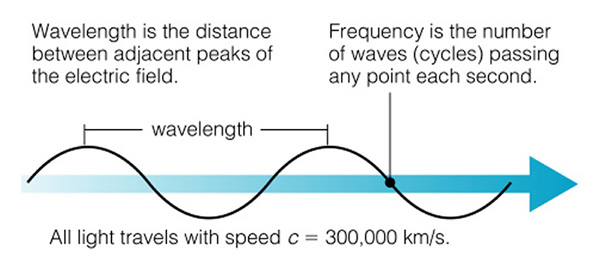
Let's remember how wavelength is defined:

Astronomers break up light using a prism (or some other optical device) and record the resulting spectrum using a camera (today it is all digital):

The combination of a prism and a camera is called a spectrograph. In the spectroscopy lab, you used a "spectroscope", a spectrograph where your eye is the detector. With a spectrograph you can record the spectra of astronomical objects. But spectra are harder to get because you have to break up the light. Generally, it takes 1,000 times longer to get a spectrum then it does an image. Thus, if you had to expose for 1 second to get an image of an object, you would have to expose for 1,000 seconds to get a spectrum. This is why astronomers keep wanting to build larger, and larger telescopes--the bigger the telescope, the more light it collects, and the easier it is to record spectra of faint objects. Using spectra, astronomers can determine the chemical composition of objects, figure out their temperature, measure the gravity of star or planet, and tell whether an object is moving. Spectroscopy is the most important tool astronomers have, since they cannot travel to an astronomical object and bring home a piece for analysis in an Earth-based lab (except for Moon rocks!).

Astronomers began using spectrographs starting in the 1860's or so to examine the spectra of astronomical objects. Due to the primitive nature of photography, only spectra of the brightest objects (stars and planets) were obtained. But even these first attempts were useful, and lead to our classification scheme for stars, and eventually to the HR diagram. While Lord Rosse had used his large telescope to finally show that some of the largest and brightest "nebulae" were composed of faint stars, we did not know very much about these nebulae--they were generally too faint for spectroscopy back then. As photographic film (actually "plates") became more sensitive, it soon became possible to take spectra of the brightest galaxies, and these spectra showed that galaxies were composed of normal stars--the spectra of galaxies were composites of all different spectral types of stars. In the bulges of spirals, or ellipticals, the spectra showed that they were mostly cool, red giant stars. In the spiral arms and in irregular galaxies, the spectra resembled those of hot, young stars. Thus, we could begin to classify galaxies--as we did a few classes ago.

After construction of the 100" telescope on Mt Wilson (in Los Angeles), shown here,

in 1917, a new, and powerful tool became available for studying galaxies. Astronomers Edwin Hubble and Vesto Slipher began to use the Mt Wilson telescope to obtain spectra of galaxies. This was very difficult work, as a typical exposure time for getting a spectrum of a galaxy could be six or seven nights. That is, they would line up the galaxy, open the shutter, expose the photographic plate all night long on one galaxy, come back the next night and do it again. They would have to do this for many nights in a row. Today we can get better spectra on smaller telescopes in a matter of minutes--but back then it was hard work.

Much to their surprise, when Hubble and Slipher examined the spectra of galaxies, they found that just about all galaxies were moving away from us (only the Andromeda galaxy was heading towards us). The galaxy spectra were "redshifted". Before we talk about why galaxies are doing this, let's talk about the Doppler effect. You are familiar with the Doppler effect--when an ambulance is coming towards you, its siren has a higher pitch, and when it passes by you, its pitch is lowered. What is happening is that the sound waves are compressed in the direction the ambulance is moving, and are stretched in the opposite direction, as shown in Figure 6.15 of the text:

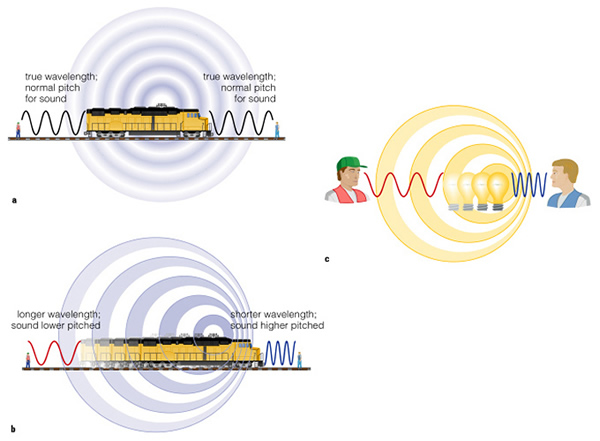
Sound travels as a wave through the air. High pitch (frequency) sounds have shorter wavelengths---they make your eardrum vibrate more rapidly (see how frequency and wavelength of sound are related here). Low pitch (frequency) sounds have a longer wavelength, and make your eardrum vibrate slowly. We detect the vibration of the eardrum as sound. A source that is emitting sound radiates sound waves into the air around it, and these sound waves travel through the air to your ear. If the source of sound is moving, the energy of the motion is added to the sound waves. If you add energy to a wave, you increase its frequency, or shorten its wavelength. Sound emitted in the opposite direction of travel has energy removed, and the wavelength of the sound is lengthened, which means its pitch is lowered. Note that the speed of the sound does not change--the speed of sound depends on the density of the medium (normally air) that it is traveling in (Animation #1, #2).

Light is also a wave just like sound--the difference is that light does not need a medium to travel in--it can travel in a vacuum (and unlike sound, you cannot go faster than the speed of light). A moving source that emits light will have a different spectrum than a non-moving source. If the source is coming towards you, the light will be blueshifted (the pitch is raised), if a light source is moving away from you, its light will be redshifted. An excellent example is shown in Figure 6.16 on page 166:

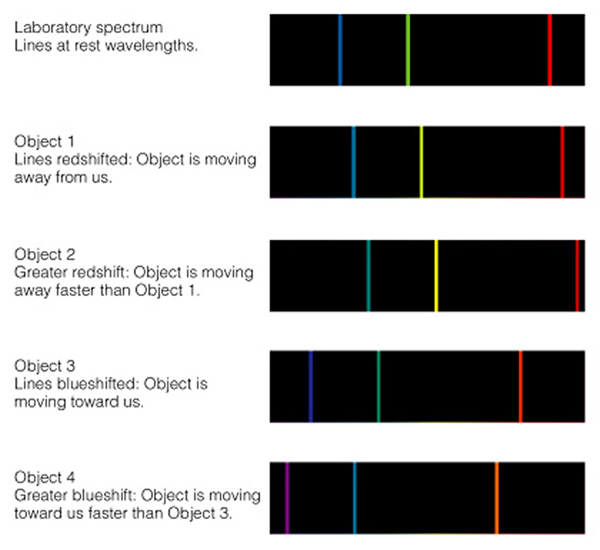
The amount of shift in wavelength depends on the speed of the object (animation). You can read more about it in the text book in Mathematical Insight 6.3 on page 166.] The faster an object is moving, the bigger the shift in wavelength. All you have to do is compare the spectrum of an object with a lamp in your spectrograph, and you can see if there is any shift in wavelength. Thus, using spectroscopy, astronomers can detect if an object is moving, and how fast that object is moving.

Back to Hubble and Slipher. These two guys were busy taking spectra of galaxies and soon noticed that every galaxy they took a spectrum of (except the Andromeda galaxy) was moving away from us! A redshifted galaxy spectrum is shown here:

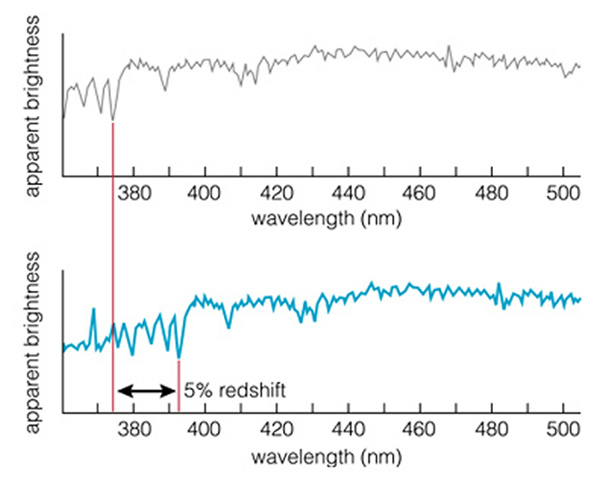
Unfortunately, it was difficult to determine how far away these galaxies were, but Hubble suspected the smaller, fainter galaxies were further away than the bigger, brighter galaxies. When he looked at the data, he found out that the more distant galaxies appeared to be moving away from us at a faster speed than the nearby galaxies! When Hubble plotted up the speed of a galaxy versus its distance, he found that there was a linear relationship between these two quantites, here is his plot:

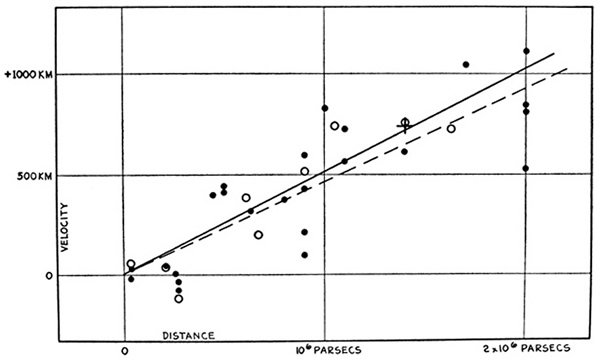
The speed of an object ("V") depends on a constant (H_o, "Hubble's constant") times its distance ("d"). If Hubble could figure out accurate distances to some galaxies, it would be possible to use this law to measure distances to all galaxies (since d = V/H_o). Thus, an enormous effort began in the 1920's to try to figure out a cosmic distance ladder to calibrate Hubble's law. The modern value of the Hubble constant has a value near H_o = 75 km/s/Mpc. Note the unusual units. Let's work an example. If a galaxy has a redshift velocity of 7,500 km/s, then its distance is d = (7,500 km/s)/(75 km/s/Mpc) = 100 Mpc. Remember that a Mpc is a mega-parsec, which is one million parsecs, or 3.26 million light years (see the class notes for class #22). [Animated graphic] Another video: Hubble's law.

While Hubble had discovered an interesting relationship, it was the implications of this discovery that were astounding: all of the galaxies in the Universe were moving away from each other! Why were they doing this? If all of the galaxies in the Universe are moving away from each other, what about the past? It seems implausible to suppose that all of the galaxies in the Universe were sitting around motionless for some extended time period and then decided to start moving. It was more probable that all of the galaxies had been moving since the time they had formed. But if this is true, we simply have to wind the clock backwards to earlier and earlier times. If we do this, we come to the conclusion that at some time in the distant past, all of the galaxies were located in the same spot! All of the galaxies in one tight little spot in space--the Universe had a beginning.

Why do we say it had a beginning? It is one of the principles of physics that any process in the Universe must be able to be reversed, that is to run both forward and backward. For example, the emission of a photon of light by a hydrogen atom run backwards is simply the absorption of a photon of light by a hydrogen atom. Thus, if we run the clock backwards we move the galaxies closer, and closer together. Eventually, the galaxies will all merge together into one super-galaxy, and then the stars and gas that made up these galaxies would be further compressed until all of the matter in the Universe was merged together to form one big soup of atomic particles--at such a time, there would not be a recognizable Universe, and thus the Universe we are familiar with today apparently did not exist at some distant time in the past. So we say that at sometime in the past, there appears to have been a beginning to the Universe.

How long ago was this? It is actually fairly simple to make a guess about when this occurred. Let's think about it for a moment. First, assume that we are at the center of the Universe (a bad assumption, but ok here). Put a galaxy at a distance of 100 Mpc from us. If so, it is moving away from us at 7,500 km/s. How long does it take for it to get that far from us? First we must change Mpc to kilometers. One mega-parsec is (1,000,000 pc) x (3.26 ly/pc) x (9.46 x 10¹² km/ly) = 3.08 x 10¹⁹ km. 100 Mpc = 3.08 x 10²¹ km. If a galaxy at 100 Mpc is moving at a velocity of 7,500 km/s, we can figure the time it takes to go that far as time = distance/velocity = 3.08 x 10²¹/7,500 = 4.11 X 10¹⁷ seconds. If you remember, there are 3.15 X 10⁷ seconds per year. So, we can convert 4.11 X 10¹⁷ seconds into years by dividing: 4.11 X 10¹⁷/3.15 X 10⁷ = 13.0 billion years. Given Hubble's law, we can estimate that the Universe is about 13 billion years old!

Remember, there is no reasonable way around this conclusion. We observe that all of the galaxies in the Universe are moving away from us. They are doing so in an amazingly uniform fashion---the Hubble law. It is very contrived to suggest that all of the galaxies were just sitting around in the Universe and then all of a sudden, collectively decided to start moving in just such a way that Hubble's law would work---how would all galaxies at 100 Mpc know to move away at 7,500 km/s, while all galaxies at 200 Mpc move away at 15,000 km/s? The better explanation is that all of the galaxies started moving at the same time in the distant past. If so, we can run the clock backwards using the Hubble constant, and estimate the age of the Universe---when everything began! We will discuss a model for this event (the "Big Bang"), and the evidence that led to this model soon. In this model, it isn't the galaxies that are moving outwards from some central point, but it is actually the entire Universe that is expanding.

But back to Olbers' paradox--remember it was the question why isn't the sky bright at night? The assumption underlying Olbers' paradox was that the Universe was infinite in size. But we can figure out how big the ("visible") Universe must be by assuming that the most distant galaxies are moving at the speed of light. If so, the most distant galaxies would be at a distance of (300,000 km/s)/(75 km/s/Mpc)= 4,000 Mpc. While 4,000 Mpc is a very big number, it is not infinite, thus the assumption that there are an infinite number of stars and galaxies out there is incorrect, and thus Olbers' paradox is resolved. In an expanding Universe, there is another, more subtle reason for why the sky the sky is not bright at night. The faster an object moves, the larger a redshift the light it emits will have. If something is moving near the speed of light, the redshift is extremely large, and any optical light will be redshifted into the radio---thus, Hubble's law also tells us that the most distant galaxies will be "too red" for us to see, thus even if there were many more galaxies in the Universe than we currently see, the most distant of these would not be detectable at optical wavelengths, and thus, they would not make the night time sky bright. Recently, a large telescope was launched into space that observes at far infrared wavelengths (that do not penetrate to the ground) to show that those highly redshifted galaxies exist:

Everything in this deep image is a galaxy! We can only detect these galaxies in the far infrared, as all of their visual light has been redshifted out to these low energies. There are so many galaxies in these deep images, we almost have an "infrared Olber's paradox"!

How about Newton's paradox? Newton's paradox was that all of the matter, if sitting around stationary, would tug on all other matter via gravity. Eventually, if given an infinite amount of time, all of the matter would start moving to some central point and collapse into one big ball of matter. But the galaxies are flying apart, not collapsing towards one another--thus, Newton's paradox is also resolved by Hubble's observation. In addition, the Universe is not infinitely old! Thus, the "Hubble expansion" eliminates Newton's paradox in two different ways!

Next, we will try to answer the questions of why the Universe is behaving in this way, what the future holds for the Universe, and talk some more about its birth.