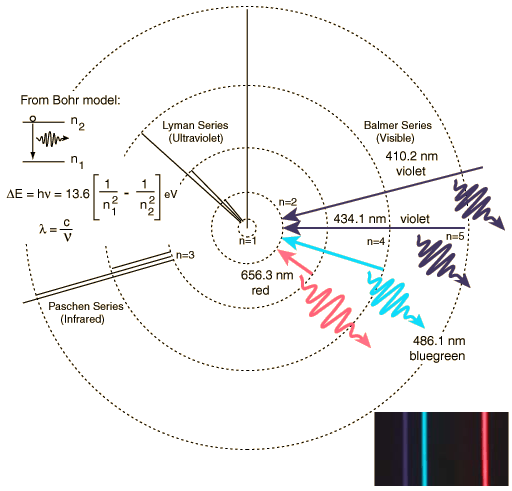
I want to briefly review atomic structure today, as it the physics of atomic processes that allow us to understand the universe around us. Let's start by remembering the structure of the atom--we have a small nucleus made up of protons and neutrons, with electrons "in orbit" around it. Protons are massive particles and have a positive electrical charge of +1 unit. Neutrons have the same mass as protons, but have no electrical charge. Electrons have a tiny mass (1/1,836 that of a proton), and have a negative electrical charge of -1 unit. It is the opposite charges of the electrons and protons that form the attraction that keeps atoms together. Here is our simplified model of the atom (the Bohr model):

Transitions of electrons between orbits creates spectral lines. An electron in an inner orbit can absorb a photon and transition to a higher orbit, or an electron in a higher orbit can emit a photon, and transition to a lower orbit. Note that these photons have specific, well-determined and precise energies--we say the radiation is quantized. This creates two of the types of spectra observed in nature, an absorption line spectrum, and an emission line spectrum:
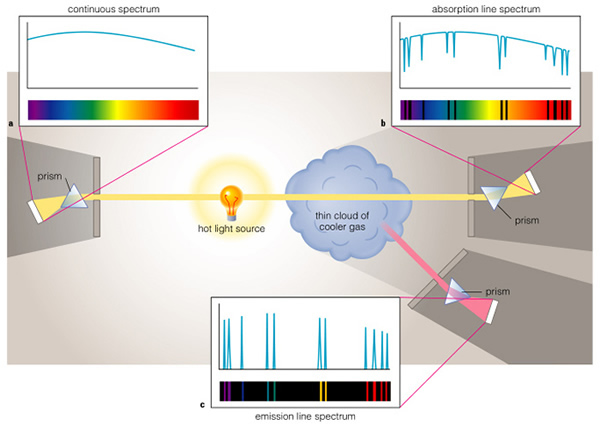
The third kind of spectrum is a continuous one, created in hot, dense objects where the nearby electrons and nuclei distort the electron orbits, creating an infinite number of possible orbits, or even partial orbits, that allow for a non-quantized type spectrum with nearly all wavelengths being represented. Light bulbs, stove top burners and stars emit continuous spectra because they are hot and dense. The temperature of the source of the continuous spectrum, however, determines the color of the source. An electric stove-top burner emits mostly red light because it is relatively cool, about 500 K (roughly 400 oF). In fact, a source this cool emits > 95% of its energy in the infrared region of the electromagnetic spectrum. A light bulb filament is quite a bit hotter, with a temperature near 2,700 K, this temperature source also emits most of its energy in the infrared, but enough occurs in the visible to be useful for indoor lighting. The Sun has a temperature of 5,800 K, it emits most of its light in the green/yellow portion of the visual band of the electromagnetic spectrum. Hotter stars emit more blue light than the Sun, while cooler stars emit more red light. We will use this fact in the next class to determine the temperatures of stars.
A continuous spectrum has a specific shape, sometimes called a thermal radiation spectrum, and is (historically) called a "blackbody spectrum". The following figure (6.13 of the text) shows the wavelength-dependent shape of the thermal spectrum:
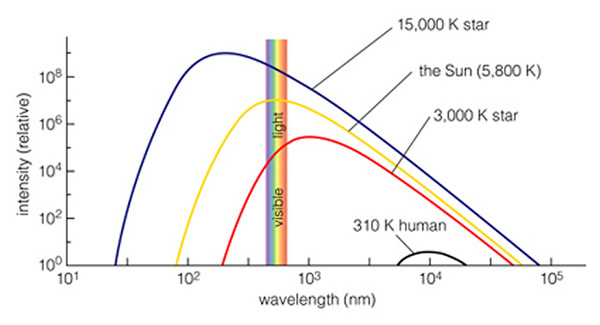
In this figure, the y-axis is a measure of how many photons are coming from the source each second (called intensity). The x-axis is in nanometers (10-9 meters). The hotter the star, the "bluer" its spectrum. The cooler the star, the "redder" its spectrum. Remember that as you transition from yellow, to green, to blue, to ultraviolet, the wavelengths of the light are getting shorter, and the individual photons contain more energy. Thus, by measuring the intensity at two or three wavelengths on the continuous spectrum curve, you can measure an object's temperature! All dense objects that have a temperature above 0 K emit thermal radiation--even humans. Our body temperature is 98.6 oF (310 K), so we emit all of our energy in the infrared (near 104 nanometers).
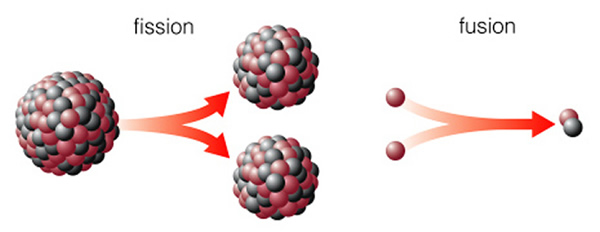
We briefly encountered nuclear fission when we were discussing radioactive decay. Nuclear fission is the instantaneous (either natural or induced) splitting of the nucleus of a high-mass element such as uranium. This diagram (figure 15.5 from the text) shows a large nucleus of protons and neutrons splitting into two smaller (daughter) nuclei:
We can use radioactive decay to determine the ages of rocks, and geologists have used this technique to determine the age of the Earth, Moon, and solar system (from meteorites). Nuclear fission can also be used to run a power plant, because when a nucleus splits, it releases energy. Nuclear fission can also be used to make an atomic bomb. Many elements with large nuclei are unstable. The reason these nuclei split is quite technical. The proper way to view it is that the force that holds the nucleus together (the strong nuclear force) only works over very short distances. As a nucleus becomes bigger, the attractive force can just barely hold the nucleus together--the nucleus can be envisioned as a vibrating sphere of jello. Wait long enough (say a "half life"), and the nucleus might spontaneously split.
Or, you can add energy to the nucleus and force it to split. How do you do the latter? If you bombard the nucleus with high energy neutrons and protons, these particles can impact a nucleus, adding energy, and causing it to break apart. This is how both nuclear reactors and atom bombs work. When a nucleus breaks apart, the pieces can then encounter other nuclei, and cause them to split. If there is sufficient unstable material (say plutonium or uranium), and nothing to stop the process, then the result can be a bomb. In a nuclear reactor, rods of a proton/neutron-absorbing material (usually cadmium) are inserted between the uranium containers to slow down the process to a manageable level. The radioactive decay generates heat, this creates steam that turns a turbine, which generates electricity.
Nuclear fusion is the opposite process. In nuclear fusion larger atomic nuclei are built from small pieces. This process is hard to manage because you need to input huge amounts of energy into the particles in order to force them to stick together. In the simplest case, two individual protons and two neutrons are joined together to form a helium nucleus. Note that protons do not want to stick together, as they both have positive charges, and positive charges repel each other ("electromagnetic repulsion"):
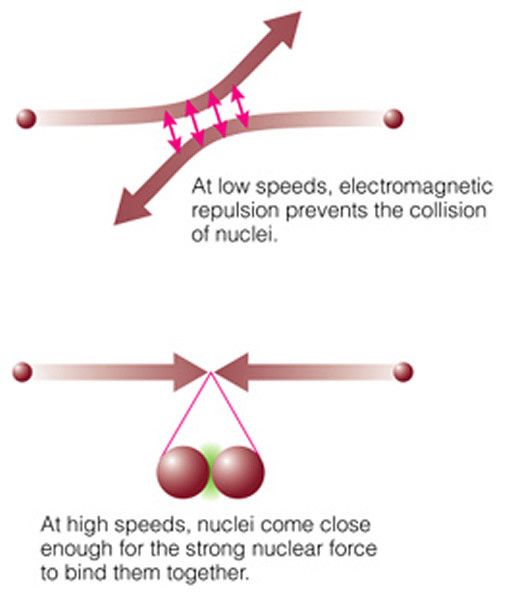
But if you can get two protons very close together, the strong nuclear force can overwhelm the electrostatic force, and the protons can stick together. The strong nuclear force is much, much stronger than the electrostatic force, but it only works over very short distances (while the electrostatic force works at ALL distances!). To get protons close enough together requires extremely high densities and temperatures--just like at the center of the Sun and the stars! The actual chain of events (the "proton-proton chain", see page 502) is shown here:
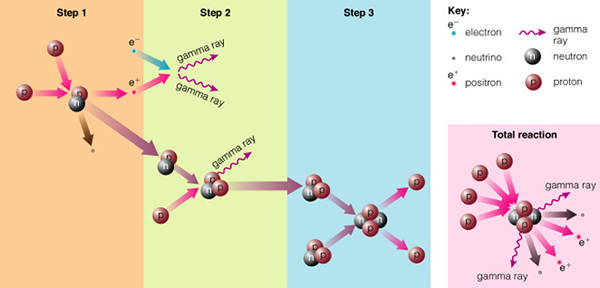
The energy released in the form of gamma-rays when two protons stick together ("step 1") act to heat the gas near the proton collision, and this in-turn heats the center of the star even more. This new nucleus, composed of one proton and one neutron (one of the protons changes to a neutron by emitting a positron), is the isotope of hydrogen called deuterium (2H). If we add another proton to this dueterium nucleus ("step 2"), we have the isotope of helium called "helium three" (3He). Normal helium is helium four (4He), containing two protons and two neutrons (shown in "step 3"). Add one more neutron, and you get helium four, a very stable nucleus (instead of just adding one more neutron, however, the more favored nuclear process is to ram two helium three nuclei together, in which helium four is produced, and two protons are expelled, as shown in the figure). In the Sun and most other stars, the hydrogen is being "burned" to produce helium. In the process, a large amount of energy is released, heating the core of the star to hotter, and hotter temperatures.
This is how the Sun and stars generate energy, the pressure at the center of the stars due to gravity generates high densities and temperatures. Gravity is relentless, constantly tugging on all the gas all of the time. Gravity tries to make the stars shrink. In the centers of stars, however, the temperature and density get so high, that protons can collide with other protons and stick together to form larger nuclei. This process releases energy, and fights gravity. We have a balance, the gravity tries to keep shrinking the star, but this shrinking generates heat, and eventually even greater amounts of energy via nuclear fusion. The heat generated in the center through nuclear fusion has to get out of the star---and in doing so it tries to make the star expand to lower density. Stars eventually reach an equilibrium size that depends on their mass, where the gravitational pressure and pressure produced by nuclear fusion are perfectly balanced. Shortly we will learn about the dramatic events that occur when this equilibrium is disturbed.
In generating the energy to power a star, all four fundamental forces of nature are involved: gravity, electromagnetic, weak nuclear, and strong nuclear. All matter pulls on all other matter through gravity--the star forms due to gravity trying to shrink the cloud of gas---gravity forms the embryonic star. As the star collapses it generates heat, this heat is radiated away through the electromagnetic force (light). Eventually, however, the center gets so hot that we can ram protons together so hard that they overpower the electromagnetic repulsion and stick together through the strong nuclear force. But some of the protons in this process turn into neutrons through "Beta decay" through the weak nuclear force. Gravity is a very weak force, but it extends over an infinite range, the strong nuclear force is by far the strongest, but it has a very limited range.
Fundamental Forces1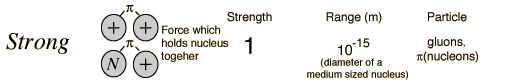 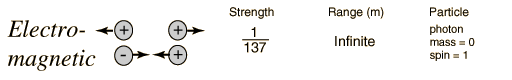 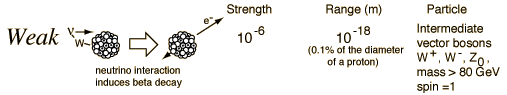 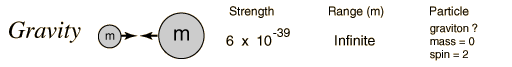 |
The reason gravity can dominate over these other forces is that it is always attractive, never repulsive. And, the other forces have balanced "charges", so they attract and cancel each other out. Gravity doesn't have this.
With a basic understanding of how stars shine, and how spectra are created, we can now try to apply our knowledge to the variety of stellar objects that exist in our Universe. The first obstacle we must overcome, however, is how do we measure the distances to stars? It is a rather easy exercise to measure the distance to the Sun, but it is much more difficult to measure the distances to other stars. On the Earth, and in the solar system, we can bounce radar beams (actually beams of microwaves) off of objects and time how long it takes for the reflected beam to return. Since we know the time the radar energy left, and the speed of light, we can easily figure out how far away an object is. This is not possible with stars. They are so far away, that it would take too long for our radar beam to return if we had a powerful enough beam to bounce off of a nearby star!
Astronomers have only one direct method to determine the distances to objects, and that is the technique of stellar parallax. By measuring the small angular shift an object exhibits as you (the observer) shift position, you can calculate how far away something is. You will be introduced to the concept of parallax in a forthcoming lab. By changing your position, foreground objects appear to shift versus the background. This is how stellar parallax works, we measure the shift of a nearby star with respect to a set of very distant background stars, and find its distance (Figure 15.3 on page 521 of the text):
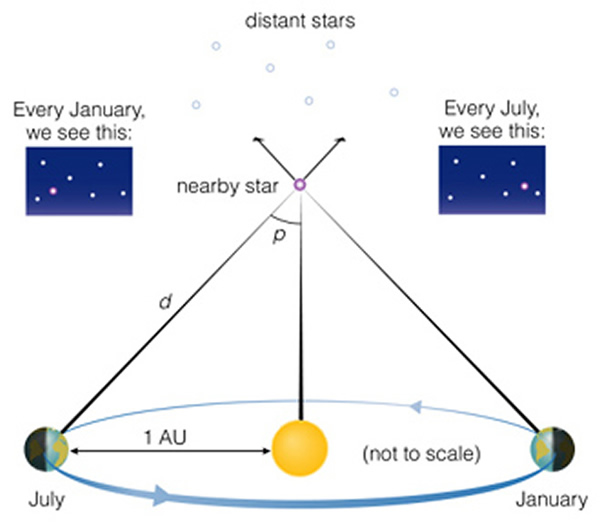
The greatest separation that we can manage while remaining on the Earth is to wait six months, and observe stars from the opposite sides of the of the Earth's orbit (giving a large "baseline"). Thus, it takes six months to observe just one parallax (Parallax animation). This process would be easy if stars were closer. But in fact, stars are so far away that the angle ("p" in the above diagram) is very, very small--the closest star (Alpha Centauri) has a parallax angle of p = 0.000214 degrees!!! Instead of using degrees, astronomers use the tiny unit of angle called an arcsecond. Earlier this semester we mentioned this unit. Let's referesh ourselves: there are 360 degrees in a circle. There are 60 arcminutes in a degree, and there are 60 arcseconds in an arcminute. Thus, one arcsecond is 1/3,600 of a degree. Using this unit, we can convert the above angle in degrees to arcseconds: "p" in arcseconds = 0.000214 x 3,600 = 0.77 arcseconds. We specify arcseconds on a number by the addition of a single quotation mark afterwards, so instead of saying 0.77 arcseconds, we write this as 0.77".
In lab you will be shown how to convert this angle to a distance, and we will not do that here (you use the trignometric tangent or sine function to do this---see the box on page 526). But we can use the handy conversion that an object with a parallax of 1" has a distance of 3.26 light years (remember that a light year is the distance light travels in a year, about 12 trillion miles--see the notes for class #1). So, Alpha Centauri is at a distance of of 3.26/0.77 = 4.23 light years ("ly"). Astronomers work with parallaxes so often that it leads to a new distance unit: the "parsec". A parsec is 3.26 ly (see page 526). The distance in parsecs is simply 1/p, where "p" is the parallax angle measured in arcseconds. An object with p = 0.1", is at a distance of 10 parsecs (1/0.1), an object with a parallax of 0.01" is at a distance of 100 parsecs (1/0.01). The word parsec derives from the words "parallax second".
We will often use parsecs instead of light years during the remainder of this class, but remember that the two are simply units of distance (like an inch, foot, mile, meter, kilometer, etc), and that a parsec is simply 3.26 x the length of a light year. When talking about our Milky Way galaxy, we will encounter the term "kiloparsecs" (1,000 parsecs), and when talking about other galaxies we will encounter "Megaparsecs" (1 million parsecs). For some reason, astronomers never use the terms kilo-light years, or mega-light years. It is just one of those traditions.
1Taken from here.