- local wavefront curvatures flat on scales of small apertures, and
- instantaneous slopes vary by
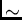 an arcsec.
an arcsec.
References: Coulson, ARAA 23,19; Beckers, ARAA 31, 13; Schroeder 16.II.
The Earth's atmosphere is turbulent and variations in the index of refraction cause the plane wavefront from distant objects to be distorted. This distortion introduces amplitude variations, positional shifts and also image degradation.
This causes two astronomical effects:
The time variation scales are several milliseconds and up.
The effect of seeing can be derived from theories of atmospheric turbulence, worked out originally by Kolmogorov, Tatarski, Fried. Here, I'll quote some pertinent results, without derivation.
A turbulent field can be described statistically by a structure function:
Kolmogorov turbulence gives:
Physically, ![]() is (roughly) inversely proportional to the image size
from seeing:
is (roughly) inversely proportional to the image size
from seeing:
Seeing is more important than diffraction at shorter wavelengths,
diffraction more important at longer wavelengths;
effect of diffraction and seeing cross over in the IR (![]() 5 microns for 4m);
the crossover falls at a shorter wavelength for smaller telescope or better
seeing.
5 microns for 4m);
the crossover falls at a shorter wavelength for smaller telescope or better
seeing.
The meat of ![]() is in
is in
![]() ; as you might expect, this varies
from site to site and also in time. At most sites, there seems to
be three regimes of ``surface layer" (wind-surface interactions
and manmade seeing), ``planetary boundary layer" ( influenced by
diurnal heating), and ``free atmosphere" (10 km is tropopause: high
wind shears), as seen in
this plot.
A typical site probably has
; as you might expect, this varies
from site to site and also in time. At most sites, there seems to
be three regimes of ``surface layer" (wind-surface interactions
and manmade seeing), ``planetary boundary layer" ( influenced by
diurnal heating), and ``free atmosphere" (10 km is tropopause: high
wind shears), as seen in
this plot.
A typical site probably has ![]() cm at 5000Å.
cm at 5000Å.
We also have to consider the coherence of the same turbulence pattern
over the sky: coherence angle call the isoplanatic angle, and region over
which the turbulence pattern is the same is called the isoplanatic patch.
In the infrared ![]() cm,
cm, ![]() m,
m, ![]() arcsec.
arcsec.
Note however, that the ``isoplanatic patch for image motion"
(not wavefront) is ![]() .
For
.
For ![]() m,
m, ![]() km,
km,
![]() arcsec.
arcsec.