Least squares fitting

We have encountered the concept of least-squares fitting several times: once to derive extinction and transformation coefficients and zero points, and again when we talked about crowded field photometry. Least squares fitting has a very large number of applications in science in general, as it is a commonly used technique to determine the parameters of some model which one wishes to fit to their data.

The concept of least-squares fitting has a statistical basis when one considers a set of observations which arise from a system which can be described by some mathematical model but where the observations have errors which are normally distributed around the predicted model values. In this case, we can write the probability of observing any particular data point given a model, $y(x)$:

$$P(y_i) \propto \exp {-0.5 (y_i - y(x_i))^2\over \sigma_i^2}$$

The total probability of observing all the data points in a data set is just the product of all of the probabilities:

$$P \propto \Pi_{i=1}^N \exp {-0.5 (y_i - y(x_i))^2\over \sigma_i^2}$$

We wish to ask the question: for what choice of model, $y(x)$, over all models which fulfill some functional form, is the total probability maximized. Maximizing the above function is the same as maximimizing its logarithm, or, alternatively, minimizing the negative of its logarithm, i.e., minimizing

$$\chi^2 \equiv \sum_{i=1}^N {(y_i - y(x_i))^2\over \sigma_i^2}$$

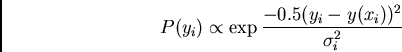
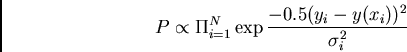
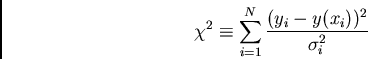
This is the standard least-squares equation: one wishes to minimize the sum of the square of the differences between observation and model by adjusting the model parameters. We define this quantity as ``chi-squared'', or $\chi^2$. For a good fit, one would expect that on average, points deviate from the model by roughly $\sigma_i$, so one would expect a $\chi^2$ for a set of $N$ observations to approach $N$ if the model is a good model and the errors have been estimated properly. In fact, it is possible given an observed value of $\chi^2$ to compute the probability that this value would be obtained if the model is correct; this allows one to judge the quality or likelihood that the model which minimizes $\chi^2$ is actually the correct model. One often discussed the reduced $\chi^2$ quantity, $\chi_\nu^2$, which is just $\chi^2$ divided by $N+M$, where $N$ is the total number of points, and $M$ is the number of free parameters in the fits; the latter is there because any set of observations which does not have more data points than the number of free parameters can generally be fit perfectly even for an incorrect model. The total $N+M$ is called the degrees-of-freedom of the fit.

How does one do least-squares in practice? Basically, one wishes to minimize $\chi^2$ with respect to one or more parameters of a model. Let us first consider models which can be written in the form:

$$y(x_i) = \sum_{i=1}^M a_k X_k(x_i)$$

In this case we can write

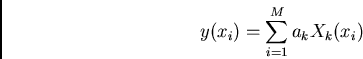
$$\chi^2 = \sum_{i=1}^N \left[ y_i - \sum_{k=1}^M a_k X_k(x_i)\over \sigma_i\right] ^2$$

We minimize by taking derivatives with respect to each parameter, $a_k$, and simulateously solving for the parameters with zero derivative with respect to each parameter. This gives us a system of $M$ equations of the form:

$$\sum_{i=1}^N 2 \left[ y_i - \sum_{k=1}^M a_k X_k(x_i)\over \sigma_i\right] (-X_m(x_i)) = 0$$

for each parameter, $m$, (and you can get rid of the negative sign as well). From this we get

$$\sum_{i=1}^N {X_m \sum_{k=1}^M a_k X_k(x_i) \over \sigma_i^2} = \sum_{i=1}^N y_i X_m(x_i)$$

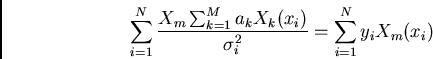
If we define a matrix, $\alpha_{kl}$, to be

$$\alpha_{km} \equiv \sum_{i=1}^N {X_m(x_i) X_k(x_i) \over \sigma_i^2}$$

and a vector, $\beta$, to be

$$\beta_{k} \equiv \sum_{i=1}^N {y_i X_k(x_i) \over \sigma_i^2}$$

then we can write:

$$\alpha_{km} a_m = \beta_k$$

This is a linear set of equations with $M$ unknowns, the $a_m$, which can be solved by standard linear algebra techniques (see, for example, Numerical Recipes, chapter 2), e.g. matrix inversion:

$$a_m = \alpha^{-1} \beta$$

Associated with solving for the ``best'' parameters, one often wishes to compute the errors associated with the fit parameters. This is discussed in Numerical Recipes (chapter 15), with the result:

$$\sigma^2 (a_m) = \alpha^{-1}_{mm}$$

One can also consider the situation where a model is non-linear in the parameters, $a_m$, i.e., the derivatives with respect to each parameter may depend on the parameter value. This leads to non-linear least squares techniques. These are more complex, as one can have situations where there are many minima in $\chi^2$ and one needs to find the global minimum rather than a local one. Such problems require a starting guess of a reasonable solution and then iteration towards the best solution. The crowded field photometry problem falls into this category because the model is nonlinear in the position parameters.