Aperture photometry

Find stars. Sum up total light. It is spread over several pixels in a form given by the point spread function $PSF(i,j)$. However, also need to estimate and subtract background.

Error estimation: we're going to sum over pixels. First just consider the object aperture:

$$S = \sum [Star(i,j) + B(i,j)] - N B$$

where the sum is over $N$ pixels, and $B$ is the background per pixel. To get the true signal $S$, $N$ would need to approach infinity since the stellar profile continues out to great distances. In practice, however, we choose $N$ such that a repeatable fraction of light falls within the $N$ pixels independent of exposure. Next, we want to determine the error in our measurement of $S$. The noise is

$$\sigma_S^2 = \sum (Star(i,j) + B(i,j) + rn^2) + N^2\sigma_B^2$$

which is just

$$\sigma_S^2 = S + \sum (B(i,j) + rn^2) = S + N (B + rn^2) + N^2\sigma_B^2$$

So now we have to consider how we will estimate $B$. In the simplest case, we just go away from the star and take then mean level. Generally, we want to minimize effects of any nonuniform background, so we consider an annulus around the star. If this annulus contains $N_a$ pixels, then

$$B = \sum_a B(i,j) / N_a$$

and

$$\sigma_B^2 = {\sum [B(i,j) + rn^2]\over N_a^2}$$

From this we see that errors in determining the background are small contributors to the total error in the star if $N_a>>N$, and generally that is the case. If the errors in determining the background are negligible, then

$$S/N = {S\over \sqrt{S + N(B+rn^2)}}$$

which is an important result.

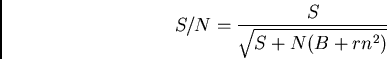
Using this, one can consider the optimal choice of aperture. Clearly, as the aperture increses, the signal-to-noise decreases, so long as you have a reasonable fraction of the total starlight; this is especially true for fainter stars. The optimal choice of aperture will depend on the brightness of the star: a larger aperture will be better for brighter stars, a smaller aperture for fainter stars. But also recall that we don't want to use a too small aperture or else we won't be able to compare results from different frames because of changes in the PSF.

This leads to the commonly used technique of using small apertures for all of the stars on the frame, but large apertures for a few bright stars. The few bright stars are assumed to have representative PSFs for this frame, so all of the small aperture measurements can be aperture corrected to large aperture measurements without the increase in noise you would get if you actually used a large aperture. Note that you can't go arbitrarily small as you will eventually run into the problem of PSF variations across the frame if for no other reason than any small dependences on pixel centering.

In fact, you can do better for S/N if you use additional information. If you know the shape of the PSF, you can use this information to fit your stellar image, increasing the S/N in the process. Simple linear least squares argument, if you know PSF and position accurately, leads to

$$\sigma_S = S + N_{eff}(B + rn^2)$$

where

$$N_{eff} = {1\over \sum PSF(i,j)^2}$$

Note that you'll improve S/N, but only if your assumption that your knowledge of the PSF is good is valid. This naturally leads into the next area of stellar photometry in crowding fields, when you are forced into fitting the PSF whether you like it or not.