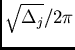 . For small apertures, you can make significant
gains with removal of just low order terms, but for large apertures you
need very high order terms.
. For small apertures, you can make significant
gains with removal of just low order terms, but for large apertures you
need very high order terms.
The goal of adaptive optics is to partially or entirely remove the effects of atmospheric seeing. Note that these day, this is to be distinguished form active optics, which works at lower frequency, and whose main goal is to remove aberrations coming from the change in telescope configuration as the telescope moves (e.g., small changes in alignment from flexure or sag of the primary mirror surface as the telescope moves). Active optics generally works as frequencies less than (usually significantly) 1 Hz, whereas adaptive optics must work at 10 to 1000 Hz. At low frequencies, the active optics can be done with actuators on the primary and secondary mirrors themselves. At the high frequencies reqiured for adaptive optics, however, these large mirrors cannot respond fast enough, so one is required to form a pupil on a smaller mirror which can be rapidly adjusted; hence adaptive optics systems are really separate astronomical instruments.
Many adaptive optics systems under development: see http://www.cfht.hawaii.edu/Instruments/Imaging/AOB/other-aosystems.html
The basic idea of an adaptive optics system is to rapidly sense the wavefront errors and then to correct for them on timescales faster than those at which the atmosphere changes. Consequently, there are really three parts to an adaptive optics system:
There are several methods used for wavefront sensing. Two ones in fairly common use among today's adaptive optics system are Shack-Hartmann sensors and wavefront curvature sensing devices. In a Shack-Hartmann sensor, an array of lenslets is put in a pupil plane and each lenslet images a small part of the pupil. Measuring image shifts between each of the images gives a measure of the local wavefront tilts. Wavefront curvature devices look at the intensity distribution in out-of focus images.
To correct wavefront errors, some sort of deformable mirror is used. These can be generically split into two categories: segmented and continuous faceplate mirrors, where the latter are more common. A deformable mirror is characterized by the number of adjustable elements: the more elements, the more correction can be done.
In general, it is almost impossible to achieve complete correction even
for ideal performance, and one needs to consider the effectiveness of
different adaptive optics systems. This effectiveness depends on the
size of the aperture, the wavelength, the number of resolution elements
on the deformable mirror, and the quality of the site.
Clearly, more resolution elements are needed for larger apertures.
Equivalently, the effectiveness of a system will decrease as the aperture
in increased for a fixed number of resolution elements. One can consider the
return as a function of zernike order corrected and aperture size. For large
telescopes, you'll only get partial correction unless a very large number
of resolution elements on the deformable mirror are available. The following
table gives the mean square amplitude, ![]() , for Kolmogorov
turbulence after removal of the first
, for Kolmogorov
turbulence after removal of the first ![]() terms; the rms phase variation
is just
terms; the rms phase variation
is just
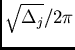 . For small apertures, you can make significant
gains with removal of just low order terms, but for large apertures you
need very high order terms.
. For small apertures, you can make significant
gains with removal of just low order terms, but for large apertures you
need very high order terms.
| n | m | Expression | Description |
|
||
| Z1 | 0 | 0 | 1 | constant | 1.030 S | |
| Z2 | 1 | 1 | tilt | 0.582 S | 0.448 S | |
| Z3 | 1 | 1 | tilt | 0.134 S | 0.448 S | |
| Z4 | 2 | 1 |
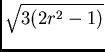 |
defocus | 0.111 S | 0.023 S |
| Z5 | 2 | 2 |
|
astigmatism | 0.0880 S | 0.023 S |
| Z6 | 2 | 2 |
|
astigmatism | 0.0648 S | 0.023 S |
| Z7 | 3 | 1 |
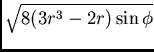 |
coma | 0.0587 S | 0.0062 5 |
| Z8 | 3 | 1 |
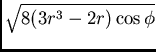 |
coma | 0.0525 S | 0.0062 S |
| Z9 | 3 | 3 |
|
trifoil | 0.0463 S | 0.0062 S |
| Z10 | 3 | 3 |
|
trifoil | 0.0401 S | 0.0062 S |
| Z11 | 4 | 0 |
 |
spherical | 0.0377S | 0.0024 S |
Another important limitation is that one needs an object on which you can derive the wavefront. Measurements of wavefront are subject to noise just like any other photon detection so bright sources may be required. This is even more evident when one considers that you need a source which is within the same isoplanatic patch as your desired object, and when you recall that the wavefront changes on time scales of milliseconds. These requirements place limitations on the amount of sky over which it is possible to get good correction. It also places limitations on the sorts of detectors which are needed in the wavefront sensors (fast readout!).
| band | Coverage (%) | ||||||
| U | 0.365 | 9.0 | .009 | .0027 | 7.4 | 1.2 | 1.8 E-5 |
| B | 0.44 | 11.4 | .011 | .0034 | 8.2 | 1.5 | 6.1 E-5 |
| V | 0.55 | 14.9 | .015 | .0045 | 9.0 | 1.9 | 2.6 E-4 |
| R | 0.70 | 20.0 | .020 | .0060 | 10.0 | 2.6 | 0.0013 |
| I | 0.90 | 27.0 | .027 | .0081 | 11.0 | 3.5 | 0.006 |
| J | 1.25 | 40 | .040 | .0120 | 12.2 | 5.1 | 0.046 |
| H | 1.62 | 55 | .055 | .0164 | 13.3 | 7.0 | 0.22 |
| K | 2.2 | 79 | .079 | .024 | 14.4 | 10.1 | 1.32 |
| L | 3.4 | 133 | .133 | .040 | 16.2 | 17.0 | 14.5 |
| M | 5.0 | 210 | .21 | .063 | 17.7 | 27.0 | 71 |
| N | 10 | 500 | .50 | .150 | 20.4 | 64 | 100 |
The isoplanatic patch limitation is severe. In many cases, we might expect non-opticmal performance if the reference object is not as close as it should be ideally. In most cases, adaptive optics worts in the partially correcting regime. This typically gives PSFs will a sharp core, but still with extended wings.
The problem of sky coverage can be avoided if one uses so-called laser guide stars. The idea is to create a star by shining a laser up into the atmosphere. To date, two generic classes of lasers have been used, Rayleigh and sodium beacons. The Rayleigh beacons work by scattering off a layer roughly 30 km above the Earth's surface; the sodium beacons work by scattering off a layer roughly 90 km above the Earth's surface. Laser guide stars still have some limitations. For one, the path through the atmosphere which the laser traverses does not exactly correspond to the path that light from a star traverses, because the latter comes from an essentially infinite distance; this leads to the effect called focal anoisoplanatism. In addition, laser guide stars cannot generally be used to track image motion since the same telescope is being used to project and record the reference image; separate tip-tilt tracking is required. In principle, all of these problems can be solved by using multiple laser guide stars with natural stars for tip-tilt, but to date, I don't know of the implementation of any such system with multiple guide stars. Systems with single laser guide stars have certainly been tested and appear to work well; but remember, only over an isoplanatic patch.
Note that even with perfect correction, one is still limited by the isoplanatic patch size. As one moves further and further away from the reference object, the correction will gradually degrade. In principle, correction over a wider field of view is possible with multiple deformable mirrors and multiple reference objects, giving rise to the concept of multi-conjugate adaptive optics systems.
Science with adaptive optics. Typical AO PSFs. Morphology vs. photometry.