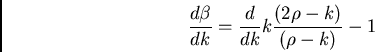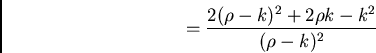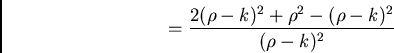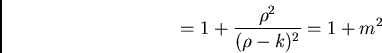Multi-surface systems

To combine surfaces, one just takes the image from the first surface as the source for the second surface, etc., for each surface. We can generally describe the basic parameters of multi-surface systems by equivalent single-surface parameters, e.g. you can define an effective focal length of a multi-surface system as the focal length of some equivalent single-surface system. The two systems (single and multi) are equivalent in the paraxial approximation ONLY.

Example: a lens (has two surfaces).

Consider a lens in air ($n\sim 1$). The first surface give

$${n\over s_1'} - {1\over s_1} = {(n-1)\over R_1} = P_1$$

The second surface gives:

$${1\over s_2'} - {n\over s_2} = {(1-n)\over R_2} = P_2$$

but we have $s_2 = s_1' - d$ (remember we have to use the plane of the second surface to measure distances for the second surface).

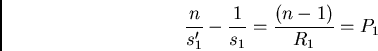
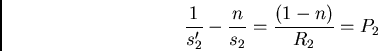
After some algebra, we find the effective focal length (from center of lens):

$$P = {1\over f'} = P_1 + P_2 - {d\over n} P_1 P_2$$

$$P = {(n-1)\over R_1} + {(1-n)\over R_2} - {d\over n} {(n-1)(1-n)\over R_1 R_2}$$

From this, we derive the thin lens formula:

$$P = {1\over f'} = {(n-1)\over R_1} + {(1-n)\over R_2} = (n-1) ({1\over R_1} - {1\over R_2})$$

$${1\over f'} = {1\over f_1} + {1\over f_2}$$

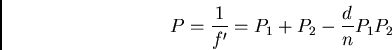
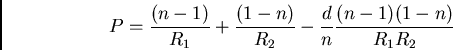
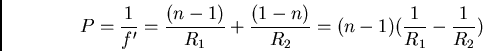
Example: a plane-parallel plate. Zero power, but moves image laterally: $\Delta = d [1-(1/n)]$.

Example: two-mirror telescopes:

In astronomy, most telescopes are two-mirror telescopes of Newtonian, Cassegrain, or Gregorian design. The Cassegrain is the most common and is outlined here First, accept some basic definitions:

• ratio of focal lengths, $\rho$:
  
  $$\rho = R_2/R_1 = f_2/f_1$$
  
  

• magnification of the secondary, $m$:
  
  $$m = -s_2' / s_2$$
  
  

• back focal distance, $f_1\beta$:
  
  $$f_1\beta = D\eta$$
  
  

• primary focal ratio, $F_1$:
  
  $$F_1 = f_1/D$$
  
  

• ratio of marginal ray heights, $k$:
  
  $$k = y_2/y_1$$
  
  

From similar triangles,

$$k \equiv {y_2\over y_1} = {s_2\over f_1} = {2 s_2\over R_1}$$

$$s_2 = {k R_1 \over 2}$$

For the secondary:

$${1\over s_2^\prime} + {1\over s_2} = {2\over R_2}$$

$$1 - m = {2 s_2^\prime\over R_2}$$

$$s_2^\prime = {R_2\over 2} (1-m)$$

Dividing these two relations gives:

$$-m = {R_2\over 2}(1-m) {2\over k R_1} = {\rho (1-m)\over k}$$

So to summarize, we get:

$$\rho = {m k \over (m-1)}$$

We also get

$$(1+\beta) = k(m+1)$$

We can derive the effective focal length and focal ratio from our thick lens formula:

$$f = f_1 m$$

$$F = F_1 m$$

So we find that the telescope basic parameters (paraxial) are determined by 3 of: $f, f_1, m, \rho, k, \beta$ (not $m,\rho,k$ or $m,\beta,k$). Usually, $f_1$ is limited by technology. Then choose $m$ to match desired scale. $k$ is related to separation of mirrors, and is a compromise between making telescope shorter and blocking out more light vs. longer and blocking less light; in either case, have to keep focal plane behind primary!

Definitions for multi-surface system:

• aperture stop: determines the amount of light reaching an image (usually the primary mirror)

• field stop: determines the angular size of the field. This is usually the detector, but for a large enough detector, it could be the secondary.

• pupil: location where rays from all field angles fill the same aperture.

• entrance pupil: image of aperture stop as seen from source object (usually the primary).

• exit pupil: image of aperture stop formed by all subsequent optical elements.

In a two-mirror telescope, the location of the exit pupil is where the image of the primary is formed by the secondary. This can be calculated using $s=d$ as the object distance (where $d$ is the separation of the mirrors), then with the reflection equation, we can solve for $s'$ which gives the location of the exit pupil relative to the secondary mirror. If one defines the quantity $\delta$, such that $f_1 \delta$ is the distance between the exit pupil and the focal plane, then (algebra not shown):

$$\delta = {m^2 k \over m +k-1} = {m^2 (1+\beta) \over m^2 + \beta}$$

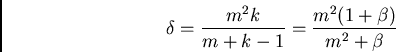
The exit pupil is an important concept. When we discuss aberrations, it is the total wavefront error at the exit pupil which gives the system aberration.

One final thing to note is how we focus a Cassegrain telescope. Most instruments are placed at a fixed location, $\beta$, behind the primary. Focussing is usually then done by moving the secondary mirror. Clearly, if you move the secondary you change $k$. Since $\rho$ is fixed by the mirror shapes, it's also clear that you change the magnification as you move the secondary; this is expected since you are changing the system focal length, $f = mf_1$. The amount of image motion for a given secondary motion is given by:

$${d\beta\over dk} = {d\over dk} k(m+1) - 1$$

where

$$m(k) = {\rho\over \rho -k}$$

so

$${d\beta\over dk} = {d\over dk} k{(2\rho -k)\over (\rho-k)} - 1$$

$$= {2 (\rho-k)^2 + 2\rho k - k^2 \over (\rho -k)^2}$$

$$= {2 (\rho-k)^2 + \rho^2 - (\rho -k)^2\over (\rho-k)^2}$$

$$= 1 + {\rho^2\over (\rho-k)^2} = 1 + m^2$$

where the motion of the secondary is $f_1 dk$ and the motion of the image plane is $f_1 d\beta$.